>>Геометрия: Сборът от ъглите на триъгълник. Пълни уроци
ТЕМА НА УРОКА: Сборът от ъглите на триъгълник.
Цели на урока:
- Затвърдяване и проверка на знанията на учениците по темата: „Сборът от ъглите на триъгълник“;
- Доказване на свойствата на ъглите на триъгълник;
- Използването на това свойство при решаването на най-простите проблеми;
- Използването на исторически материал за развитието на познавателната активност на учениците;
- Насаждане на умение за точност при изграждането на чертежи.
Цели на урока:
- Проверете способността на учениците да решават проблеми.
План на урока:
- триъгълник;
- Теорема за сбора от ъглите на триъгълник;
- Примерна задача.
Триъгълник.
Файл: O.gif Триъгълник- най-простият многоъгълник с 3 върха (ъгли) и 3 страни; част от равнина, ограничена от три точки и три отсечки, свързващи тези точки по двойки.
Три точки в пространството, които не лежат на една права, съответстват на една и само една равнина.
Всеки многоъгълник може да бъде разделен на триъгълници - този процес се нарича триангулация.
Има раздел от математиката, изцяло посветен на изучаването на моделите на триъгълници - Тригонометрия.
Теорема за сумата от ъглите на триъгълник.
Файл:T.gif Теоремата за сбора на ъглите на триъгълника е класическа теорема в евклидовата геометрия, която гласи, че сборът от ъглите на триъгълник е 180°. 
доказателство" :
Нека е дадено Δ ABC. Нека начертаем права, успоредна на (AC) през върха B и отбележим точката D върху нея, така че точките A и D да лежат на противоположните страни на правата BC. Тогава ъгълът (DBC) и ъгълът (ACB) са равни като вътрешни кръстове, лежащи на успоредни прави BD и AC и секущата (BC). Тогава сумата от ъглите на триъгълника при върховете B и C е равна на ъгъла (ABD). Но ъгълът (ABD) и ъгълът (BAC) при върха A на триъгълник ABC са вътрешно едностранни с успоредни прави BD и AC и секуща (AB), а сборът им е 180°. Следователно сборът от ъглите на триъгълник е 180°. Теоремата е доказана.

Последствия.
Външният ъгъл на триъгълник е равен на сбора от двата ъгъла на триъгълника, които не са съседни на него.
Доказателство:
Нека е дадено Δ ABC. Точка D лежи на правата AC така, че A лежи между C и D. Тогава BAD е външен за ъгъла на триъгълника при върха A и A + BAD = 180°. Но A + B + C = 180° и следователно B + C = 180° – A. Следователно BAD = B + C. Следствието е доказано.

Последствия.
Външен ъгъл на триъгълник е по-голям от всеки ъгъл на триъгълника, който не е съседен на него.
Задача.
Външният ъгъл на триъгълник е ъгълът, съседен на всеки ъгъл на този триъгълник. Докажете, че външен ъгъл на триъгълник е равен на сбора от два ъгъла на триъгълника, които не са съседни на него.  (Фиг. 1)
(Фиг. 1)
Решение:
Нека в Δ ABC ∠DAC е външен (фиг.1). Тогава ∠DAC=180°-∠BAC (според свойството на съседните ъгли), съгласно теоремата за сумата от ъглите на триъгълник ∠B+∠C =180°-∠BAC. От тези равенства получаваме ∠DAC=∠B+∠C
Интересен факт:
Сборът от ъглите на триъгълник :
В геометрията на Лобачевски сумата от ъглите на триъгълника винаги е по-малка от 180. В геометрията на Евклид тя винаги е равна на 180. В Риманова геометрия сборът от ъглите на триъгълник винаги е по-голям от 180.
От историята на математиката:
Евклид (III в. пр. н. е.) в съчинението „Начала” дава следното определение: „Успоредни са прави линии, които се намират в една и съща равнина и като са удължени неограничено от двете страни, не се срещат една с друга от никоя страна”.
Посидоний (1 век пр.н.е.) „Две прави линии, лежащи в една равнина, на еднакво разстояние една от друга“
Древногръцкият учен Пап (III в. пр. н. е.) въвежда символа на успоредните прави - знак =. Впоследствие английският икономист Рикардо (1720-1823) използва този символ като знак за равенство.
Едва през 18 век започват да използват символа на успоредните линии - знака ||.
Живата връзка между поколенията не се прекъсва нито за миг, всеки ден учим опита, натрупан от нашите предци. Древните гърци, въз основа на наблюдения и практически опит, направиха изводи, изразиха хипотези и след това на срещи на учени - симпозиуми (буквално "празник") - се опитаха да обосноват и докажат тези хипотези. По това време се формира твърдението: „В спора се ражда истината“.
Въпроси:
- Какво е триъгълник?
- Какво казва теоремата за сумата на триъгълника?
- Какъв е външният ъгъл на триъгълника?
Сборът от ъглите на триъгълник- важна, но доста проста тема, която се преподава в 7 клас по геометрия. Темата се състои от теорема, кратко доказателство и няколко логически следствия. Познаването на тази тема помага при решаването на геометрични проблеми при последващото изучаване на темата.
Теорема - какви са ъглите на произволен триъгълник, сгънат заедно?
Теоремата гласи - ако вземете произволен триъгълник, независимо от вида му, сумата от всички ъгли неизменно ще бъде 180 градуса. Това се доказва по следния начин:
- например вземете триъгълника ABC, начертайте права линия през точката B, разположена отгоре, и я обозначете като „a“, докато правата линия „a“ е строго успоредна на страната AC;
- между правата линия "а" и страните AB и BC обозначават ъглите, като ги маркират с числата 1 и 2;
- ъгъл 1 се признава за равен на ъгъл A, а ъгъл 2 е равен на ъгъл C, тъй като тези ъгли се считат за разположени на кръст;
- по този начин сумата между ъгли 1, 2 и 3 (която е посочена на мястото на ъгъл B) се признава за равна на разгънатия ъгъл с върха B - и е 180 градуса.
Ако сумата от ъглите, обозначени с числата, е 180 градуса, тогава сумата от ъглите A, B и C се признава за равна на 180 градуса. Това правило е вярно за всеки триъгълник.
Какво следва от геометричната теорема
Обичайно е да се отделят няколко следствия от горната теорема.
- Ако задачата разглежда триъгълник с прав ъгъл, тогава един от неговите ъгли ще бъде по подразбиране 90 градуса, а сборът от острите ъгли също ще бъде 90 градуса.
- Ако говорим за правоъгълен равнобедрен триъгълник, тогава неговите остри ъгли, общо 90 градуса, поотделно ще бъдат равни на 45 градуса.
- Равностранен триъгълник се състои от три равни ъгъла, съответно всеки от тях ще бъде равен на 60 градуса, а общо те ще бъдат 180 градуса.
- Външният ъгъл на всеки триъгълник ще бъде равен на сумата между двата вътрешни ъгъла, които не са съседни на него.
Можем да изведем следното правило - във всеки от триъгълниците има поне два остри ъгъла. В някои случаи триъгълникът се състои от три остри ъгъла и ако има само два, тогава третият ъгъл ще бъде тъп или прав.
Триъгълникът е многоъгълник с три страни (три ъгъла). Най-често страните се обозначават с малки букви, съответстващи на главните букви, които обозначават противоположни върхове. В тази статия ще се запознаем с видовете тези геометрични фигури, теорема, която определя каква е сумата от ъглите на триъгълника.
Видове по големина на ъглите
Има следните видове многоъгълници с три върха:
- остър ъгъл, в който всички ъгли са остри;
- правоъгълник, който има един прав ъгъл, с неговите генератори, се наричат крака, а страната, която е разположена срещу правия ъгъл, се нарича хипотенуза;
- тъп, когато е сам;
- равнобедрен, в който две страни са равни и се наричат странични, а третата е основата на триъгълника;
- равностранен, имащ и трите равни страни.

Имоти
Разпределете основните свойства, които са характерни за всеки тип триъгълник:
- срещу по-голямата страна винаги има по-голям ъгъл и обратното;
- противоположните страни с еднакъв размер са равни ъгли и обратното;
- всеки триъгълник има два остри ъгъла;
- външен ъгъл е по-голям в сравнение с всеки вътрешен ъгъл, който не е съседен на него;
- сумата от всеки два ъгъла винаги е по-малка от 180 градуса;
- Външен ъгъл е равен на сбора от другите два ъгъла, които не се пресичат с него.
Теорема за сбора на ъглите на триъгълник
Теоремата гласи, че ако съберете всички ъгли на дадена геометрична фигура, която се намира в евклидовата равнина, тогава тяхната сума ще бъде 180 градуса. Нека се опитаме да докажем тази теорема.
Нека имаме произволен триъгълник с върхове на KMN.

Начертайте KN през върха M (тази права се нарича още Евклидова линия). Маркираме точка A върху него по такъв начин, че точките K и A да са разположени от различни страни на правата MN. Получаваме равни ъгли AMN и KNM, които, подобно на вътрешните, лежат на кръст и се образуват от секущата MN заедно с правите KH и MA, които са успоредни. От това следва, че сумата от ъглите на триъгълника, разположени във върховете M и H, е равна на размера на ъгъла KMA. И трите ъгъла съставляват сбора, който е равен на сбора от ъглите KMA и MKN. Тъй като тези ъгли са вътрешни едностранни по отношение на успоредни прави KN и MA със секуща KM, сборът им е 180 градуса. Теоремата е доказана.
Последица
От доказаната по-горе теорема следва следното: всеки триъгълник има два остри ъгъла. За да докажем това, нека приемем, че дадена геометрична фигура има само един остър ъгъл. Може също да се приеме, че нито един от ъглите не е остър. В този случай трябва да има поне два ъгъла, които са равни или по-големи от 90 градуса. Но тогава сумата от ъглите ще бъде по-голяма от 180 градуса. Но това не може да бъде, защото според теоремата сумата от ъглите на триъгълник е 180 ° - не повече и не по-малко. Ето това трябваше да се докаже.
Външен ъглов имот
Каква е сумата от ъглите на триъгълник, които са външни? На този въпрос може да се отговори по един от двата начина. Първото е, че е необходимо да се намери сумата от ъглите, които са взети по един във всеки връх, тоест три ъгъла. Второто предполага, че трябва да намерите сумата от всичките шест ъгъла при върховете. Първо, нека се справим с първия вариант. И така, триъгълникът съдържа шест външни ъгъла - по два във всеки връх.

Всяка двойка има равни ъгли, защото са вертикални:
∟1 = ∟4, ∟2 = ∟5, ∟3 = ∟6.
Освен това е известно, че външният ъгъл на триъгълника е равен на сумата от два вътрешни, които не се пресичат с него. следователно
∟1 = ∟A + ∟C, ∟2 = ∟A + ∟B, ∟3 = ∟B + ∟C.
От това се оказва, че сумата от външните ъгли, които се вземат един по един близо до всеки връх, ще бъде равна на:
∟1 + ∟2 + ∟3 = ∟A + ∟C + ∟A + ∟B + ∟B + ∟C = 2 x (∟A + ∟B + ∟C).
Като се има предвид, че сборът от ъглите е 180 градуса, може да се твърди, че ∟A + ∟B + ∟C = 180°. И това означава, че ∟1 + ∟2 + ∟3 = 2 x 180° = 360°. Ако се използва вторият вариант, тогава сборът от шестте ъгъла ще бъде съответно два пъти по-голям. Тоест сумата от външните ъгли на триъгълника ще бъде:
∟1 + ∟2 + ∟3 + ∟4 + ∟5 + ∟6 = 2 x (∟1 + ∟2 + ∟2) = 720°.
Правоъгълен триъгълник
Какъв е сборът от ъглите на правоъгълен триъгълник, които са остри? Отговорът на този въпрос отново следва от теоремата, която гласи, че сборът на ъглите в триъгълника е 180 градуса. И нашето твърдение (свойство) звучи така: в правоъгълен триъгълник острите ъгли се събират до 90 градуса. Нека докажем, че е истина.

Нека ни е даден триъгълник KMN, в който ∟Н = 90°. Необходимо е да се докаже, че ∟K + ∟M = 90°.
И така, според теоремата за сумата на ъглите, ∟К + ∟М + ∟Н = 180°. Нашето условие гласи, че ∟Н = 90°. Оказва се, че ∟K + ∟M + 90° = 180°. Тоест ∟K + ∟M = 180° - 90° = 90°. Точно това трябваше да докажем.
В допълнение към горните свойства на правоъгълен триъгълник можете да добавите следното:
- ъглите, които лежат срещу краката, са остри;
- хипотенузата е триъгълна повече от всеки от краката;
- сборът на краката е по-голям от хипотенузата;
- катетът на триъгълника, който лежи срещу ъгъла от 30 градуса, е половината от хипотенузата, тоест е равен на половината от нея.
Като друго свойство на тази геометрична фигура може да се разграничи Питагоровата теорема. Тя заявява, че в триъгълник с ъгъл 90 градуса (правоъгълен) сборът от квадратите на катетите е равен на квадрата на хипотенузата.
Сборът от ъглите на равнобедрен триъгълник
По-рано казахме, че многоъгълник с три върха и две равни страни се нарича равнобедрен. Това свойство на дадена геометрична фигура е известно: ъглите в основата й са равни. Нека го докажем.
Вземете триъгълника KMN, който е равнобедрен, KN е неговата основа.

От нас се изисква да докажем, че ∟K = ∟H. И така, нека кажем, че MA е ъглополовяща на нашия триъгълник KMN. Триъгълникът MCA, като се вземе предвид първият знак за равенство, е равен на триъгълника MCA. А именно, по условие е дадено, че KM = NM, MA е обща страна, ∟1 = ∟2, тъй като MA е ъглополовяща. Използвайки факта, че тези два триъгълника са равни, можем да твърдим, че ∟K = ∟Н. Така че теоремата е доказана.
Но ни интересува каква е сумата от ъглите на триъгълник (равнобедрен). Тъй като в това отношение тя няма свои собствени особености, ще започнем от теоремата, разгледана по-рано. Тоест можем да кажем, че ∟K + ∟M + ∟H = 180°, или 2 x ∟K + ∟M = 180° (тъй като ∟K = ∟H). Няма да доказваме това свойство, тъй като самата теорема за сумата от ъгли на триъгълник беше доказана по-рано.
В допълнение към разгледаните свойства за ъглите на триъгълник, има и такива важни твърдения:
- в който е бил спуснат до основата, е едновременно медианата, ъглополовящата на ъгъла, който е между равни страни, както и неговата основа;
- медианите (ъглополовящи, височини), които са начертани към страните на такава геометрична фигура, са равни.
Равностранен триъгълник
Нарича се още прав, това е триъгълникът, в който всички страни са равни. Следователно ъглите също са равни. Всеки от тях е 60 градуса. Нека докажем това свойство.
Да кажем, че имаме триъгълник KMN. Знаем, че KM = NM = KN. А това означава, че според свойството на ъглите, разположени при основата в равнобедрен триъгълник, ∟К = ∟М = ∟Н. Тъй като според теоремата сборът от ъглите на триъгълника е ∟К + ∟М + ∟Н = 180°, то 3 x ∟К = 180° или ∟К = 60°, ∟М = 60°, ∟Н = 60°. Така твърдението е доказано.

Както може да се види от горното доказателство, базирано на теоремата, сборът от ъглите, както сборът от ъглите на всеки друг триъгълник, е 180 градуса. Няма нужда да доказваме отново тази теорема.
Има и такива свойства, характерни за равностранен триъгълник:
- медианата, ъглополовящата, височината в такава геометрична фигура са еднакви, а дължината им се изчислява като (a x √3): 2;
- ако опишете кръг около даден многоъгълник, тогава неговият радиус ще бъде равен на (a x √3): 3;
- ако впишете кръг в равностранен триъгълник, тогава неговият радиус ще бъде (a x √3): 6;
- площта на тази геометрична фигура се изчислява по формулата: (a2 x √3): 4.
тъп триъгълник
По дефиниция един от неговите ъгли е между 90 и 180 градуса. Но като се има предвид, че другите два ъгъла на тази геометрична фигура са остри, можем да заключим, че те не надвишават 90 градуса. Следователно теоремата за сбора от ъгли на триъгълник работи при изчисляване на сбора от ъгли в тъп триъгълник. Оказва се, че можем спокойно да кажем, въз основа на гореспоменатата теорема, че сборът от ъглите на тъп триъгълник е 180 градуса. Отново, тази теорема не се нуждае от повторно доказване.
Доказателство
Позволявам ABC" е произволен триъгълник. Да преминем отгоре б права линия, успоредна на права линия AC (такава права линия се нарича евклидова права линия). Маркирайте точка върху негод така че точкитеА Ид лежат от противоположните страни на права линия пр.н.е.Ъгли DBCИ ACBравен като вътрешен кръст, лежащ от секуща пр.н.ес успоредни линии ACИ BD. Следователно сумата от ъглите на триъгълник при върховете бИ СЪСравен на ъгъла ABD.Сборът от трите ъгъла на триъгълника е равен на сбора от ъглите ABDИ BAC. Тъй като тези ъгли са вътрешни едностранни за успоредни ACИ BDпри секанс AB, тогава техният сбор е 180°. Теоремата е доказана.
Последствия
От теоремата следва, че всеки триъгълник има два остри ъгъла. Наистина, прилагайки доказателството от противно, да предположим, че триъгълникът има само един остър ъгъл или изобщо няма остри ъгли. Тогава този триъгълник има поне два ъгъла, всеки от които е най-малко 90°. Сумата от тези ъгли е не по-малка от 180°. Но това е невъзможно, тъй като сборът от всички ъгли на триъгълника е 180°. Q.E.D.
Обобщение към симплексната теория
Къде е ъгълът между лицата i и j на симплекса.
Бележки
- На сфера сумата от ъглите на триъгълник винаги надвишава 180 °, разликата се нарича сферичен излишък и е пропорционална на площта на триъгълника.
- В равнината на Лобачевски сумата от ъглите на триъгълника винаги е по-малка от 180°. Разликата също е пропорционална на площта на триъгълника.
Вижте също
Фондация Уикимедия. 2010 г.
- Тейлър
- Долен лебедов мост
Вижте каква е "Теоремата за сумата от ъглите на триъгълник" в други речници:
Теорема за сумата на многоъгълни ъгли- Свойство на многоъгълниците в евклидовата геометрия: Сумата от ъглите n на многоъгълник е 180°(n 2). Съдържание 1 Доказателство 2 Забележка ... Wikipedia
Питагорова теорема- Питагоровата теорема е една от основните теореми на евклидовата геометрия, установяваща връзката между страните на правоъгълен триъгълник. Съдържание 1 ... Уикипедия
Площ на триъгълник
Питагорова теорема- Питагоровата теорема е една от основните теореми на евклидовата геометрия, установяваща връзката между страните на правоъгълен триъгълник. Съдържание 1 Твърдения 2 Доказателства ... Wikipedia
Косинусова теорема- Косинусовата теорема е обобщение на Питагоровата теорема. Квадратът на една страна на триъгълник е равен на сумата от квадратите на другите му две страни, без да се удвоява произведението на тези страни по косинуса на ъгъла между тях. За плосък триъгълник с страни a,b,cи ъгъл α ... ... Wikipedia
Триъгълник- Този термин има други значения, вижте Триъгълник (значения). Триъгълник (в евклидовото пространство) е геометрична фигура, образувана от три отсечки, които свързват три нелинейни точки. Три точки, ... ... Уикипедия
Признаци за равенство на триъгълници- Стандартна нотация Триъгълникът е най-простият многоъгълник, който има 3 върха (ъгли) и 3 страни; част от равнина, ограничена от три точки, които не лежат на една и съща права линия, и три отсечки, свързващи тези точки по двойки. Върховете на триъгълник ... Wikipedia
Евклид- древногръцки математик. Работил в Александрия през III век. пр.н.е д. Основното произведение "Начала" (15 книги), съдържащо основите на древната математика, елементарна геометрия, теория на числата, обща теория на отношенията и метод за определяне на площи и обеми, ... ... енциклопедичен речник
EUCLID- (починал между 275 и 270 г. пр.н.е.) древногръцки математик. Информация за времето и мястото на неговото раждане не е достигнала до нас, но е известно, че Евклид е живял в Александрия и разцветът на неговата дейност пада върху управлението на Птолемей I в Египет ... ... Голям енциклопедичен речник
НЕЕВКЛИДОВА ГЕОМЕТРИЯ- геометрия, подобна на геометрията на Евклид по това, че определя движението на фигурите, но се различава от евклидовата геометрия по това, че един от нейните пет постулата (втори или пети) е заменен с нейното отрицание. Отричане на един от постулатите на Евклид ... ... Енциклопедия на Collier
Триъгълник . Остроъгълни, тъпоъгълни и правоъгълни триъгълници.
Катетите и хипотенузата. Равнобедрен и равностранен триъгълник.
Сборът от ъглите на триъгълник.
Външният ъгъл на триъгълника. Признаци за равенство на триъгълници.
Прекрасни линии и точки в триъгълник: височини, медиани,
ъглополовящи, медианад перпендикуляри, ортоцентър,
център на тежестта, център на описаната окръжност, център на вписаната окръжност.
Питагорова теорема. Съотношението на страните на произволен триъгълник.
Триъгълник е многоъгълник с три страни (или три ъгъла). Страните на триъгълника често се обозначават с малки букви, които съответстват на главните букви, които обозначават противоположни върхове.
Ако и трите ъгъла са остри (фиг. 20), тогава това остроъгълен триъгълник
. Ако един от ъглите е прав(C, фиг.21), това е правоъгълен триъгълник; страниa , bобразуващи прав ъгъл се наричат крака; страна° Ссрещу прав ъгъл се нарича хипотенуза. Ако един оттъпи ъгли ( B, фиг.22), това е тъп триъгълник.
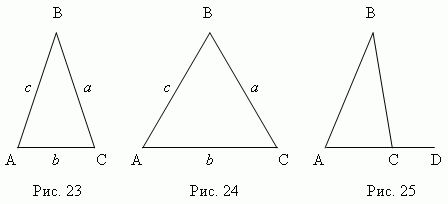
Триъгълник ABC (фиг. 23) - равнобедрен, Ако двестраните му са равниа=
° С); тези равни страни се наричат страничен, третото лице се обажда базатриъгълник. Триъгълник ABC (фиг. 24) - равностранен,
Ако всичкостраните му са равниа
=
b
=
° С). Общо взето ( а ≠ b ≠ ° С)
ние имаме скалентриъгълник .
Основни свойства на триъгълниците. Във всеки триъгълник:
1. Срещу по-голямата страна има по-голям ъгъл и обратно.
2. Срещу равни страни лежат равни ъгли и обратно.
По-специално, всички ъгли в равностранентриъгълник са равни.
3. Сборът от ъглите на триъгълник е 180 º .
От последните две свойства следва, че всеки ъгъл в равностранен
триъгълник е 60 º.
4. Продължавайки една от страните на триъгълника (AC, фиг. 25), получаваме външен
ъгъл BCD . Външният ъгъл на триъгълник е равен на сбора от вътрешните ъгли,
не е свързано с него :BCD=A+B.
5. Всякакви страна на триъгълник е по-малка от сбора на другите две страни и повече
техните различия (а < b + ° С, а > b – ° С;b < а + ° С, b > а – ° С;° С < а + b,° С > а – b).
Признаци за равенство на триъгълници.
Триъгълниците са еднакви, ако са съответно равни:
а ) две страни и ъгълът между тях;
b ) два ъгъла и прилежащата към тях страна;
в) три страни.
Признаци за равенство на правоъгълни триъгълници.
две правоъгълентриъгълниците са еднакви, ако е вярно едно от следните условия:
1) краката им са равни;
2) катетът и хипотенузата на единия триъгълник са равни на катета и хипотенузата на другия;
3) хипотенузата и острия ъгъл на единия триъгълник са равни на хипотенузата и острия ъгъл на другия;
4) катетът и прилежащият му остър ъгъл на единия триъгълник са равни на катета и прилежащия му остър ъгъл на другия;
5) кракът и противоположният остър ъгъл на един триъгълник са равни на крака и срещу острия ъгъл на другия.
Прекрасни линии и точки в триъгълник.
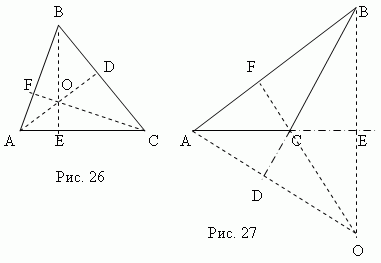
Височина триъгълник еперпендикулярен,изпуснат от произволен връх на противоположната страна ( или нейното продължение). Тази страна се наричаосновата на триъгълника . Трите височини на триъгълник винаги се пресичатв един моментНаречен ортоцентъртриъгълник. Ортоцентърът на остър триъгълник (точкаО , фиг. 26) се намира вътре в триъгълника иортоцентър на тъп триъгълник (точкаО , фиг.27) – отвън; Ортоцентърът на правоъгълен триъгълник съвпада с върха на правия ъгъл.
Медиана - Това линейна отсечка , свързващ произволен връх на триъгълник със средата на срещуположната страна. Три медиани на триъгълник (AD, BE, CF, фиг.28) се пресичат в една точка О , който винаги лежи вътре в триъгълникаи да си негов център на тежестта. Тази точка разделя всяка медиана 2:1 от върха.
Симетрала - Това ъглополовяща отсечкаъгъл от върха до точката пресичане с противоположната страна. Три ъглополовящи на триъгълник (AD, BE, CF, фиг.29) се пресичат в една точка О, винаги лежи вътре в триъгълникИ същество център на вписан кръг(виж раздел „Вписани описани многоъгълници).
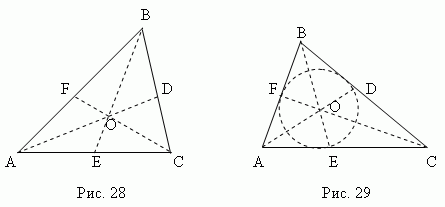
Симетралата разделя противоположната страна на части, пропорционални на съседните страни ; например на фиг.29 AE : CE = AB : BC .
Среден перпендикуляр е перпендикуляр, изтеглен от среднатасегментни точки (страни). Три ъглополовящи на триъгълник ABC(KO, MO, NO, фиг.30 ) се пресичат в една точка O, която е център описана окръжност (точки K, M, N средите на страните на триъгълник ABC).

В остър триъгълник тази точка лежи вътре в триъгълника; в тъпа - отвън; в правоъгълник - в средата на хипотенузата. Ортоцентър, център на тежестта, център на описаната и център на вписаната окръжност съвпадат само в равностранен триъгълник.
Питагорова теорема. В правоъгълен триъгълник, квадратът на дължинатаХипотенузата е равна на сумата от квадратите на дължините на катетите.
Доказателството на Питагоровата теорема очевидно следва от фиг.31. Да разгледаме правоъгълен триъгълник ABC с крака a , bи хипотенуза ° С.
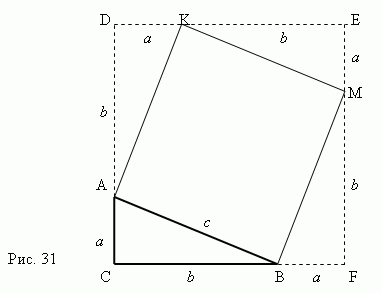
Нека построим квадратАКМБ използвайки хипотенузата AB като страна. Тогаваразширете страните на правоъгълен триъгълник ABC така че да се получи квадрат CDEF , чиято страна е равна наa + b .Сега е ясно, че площта на квадрат CDEF е ( a+b) 2 . От друга страна това площта е равна на суматаобласти четири правоъгълни триъгълникаи квадрат AKMB , т.е
° С 2 + 4 (аб / 2) = ° С 2 + 2 аб,
оттук,
° С 2 + 2 аб= (a+b) 2 ,
и накрая имаме:
° С 2 =а 2 +б 2 .
Съотношението на страните на произволен триъгълник.
В общия случай (за произволен триъгълник) имаме:
° С 2 =а 2 +б 2 – 2аб· cos ° С,
където C - ъгъл между странитеаИ b .