ما هو مجموع الزوايا؟ ما هو مجموع زوايا المضلع المحدب؟

>> الهندسة: مجموع زوايا المثلث. دروس كاملة

موضوع الدرس: مجموع زوايا المثلث.

أهداف الدرس:

• تعزيز واختبار معرفة الطلاب حول موضوع: "مجموع زوايا المثلث"؛
• إثبات خصائص زوايا المثلث.
• تطبيق هذه الخاصية في حل المسائل البسيطة؛
• استخدام المادة التاريخية لتنمية النشاط المعرفي لدى الطلاب.
• -غرس مهارة الدقة عند إنشاء الرسومات.

أهداف الدرس:

• اختبار مهارات حل المشكلات لدى الطلاب.

خطة الدرس:

1. مثلث؛
2. نظرية مجموع زوايا المثلث؛
3. المهام سبيل المثال.

مثلث.

ملف:مثلث O.gif- أبسط مضلع له 3 رؤوس (زوايا) و3 جوانب؛ جزء من المستوى يحده ثلاث نقاط وثلاثة أجزاء تربط هذه النقاط في أزواج.
ثلاث نقاط في الفضاء لا تقع على نفس الخط المستقيم تتوافق مع مستوى واحد فقط.
يمكن تقسيم أي مضلع إلى مثلثات - وتسمى هذه العملية التثليث.
هناك قسم في الرياضيات مخصص بالكامل لدراسة قوانين المثلثات - علم المثلثات.

نظرية مجموع زوايا المثلث.

ملف:T.gif نظرية مجموع زوايا المثلث هي نظرية كلاسيكية في الهندسة الإقليدية تنص على أن مجموع زوايا المثلث هو 180 درجة.

دليل" :

دع Δ ABC يعطى. لنرسم خطًا موازيًا لـ (AC) عبر الرأس B ونضع علامة على النقطة D عليه بحيث تقع النقطتان A وD على طرفي نقيض من الخط BC. ثم تكون الزاوية (DBC) والزاوية (ACB) متساوية بالعرض الداخلي مع الخطوط المتوازية BD وAC والقاطع (BC). إذن مجموع زوايا المثلث عند الرؤوس B و C يساوي الزاوية (ABD). لكن الزاوية (ABD) والزاوية (BAC) عند الرأس A للمثلث ABC هما من جانب واحد داخليًا وبهما خطان متوازيان BD وAC والقاطع (AB)، ومجموعهما 180 درجة. وبالتالي فإن مجموع زوايا المثلث هو 180 درجة. لقد تم إثبات النظرية.

عواقب.

الزاوية الخارجية للمثلث تساوي مجموع زاويتين غير مجاورتين للمثلث.

دليل:

دع Δ ABC يعطى. تقع النقطة D على الخط AC بحيث تقع A بين C وD. إذن BAD تقع خارج زاوية المثلث عند الرأس A وA + BAD = 180°. لكن A + B + C = 180°، وبالتالي B + C = 180° – A. وبالتالي BAD = B + C. وقد تم إثبات النتيجة الطبيعية.

عواقب.

الزاوية الخارجية للمثلث أكبر من أي زاوية في المثلث غير مجاورة لها.

مهمة.

الزاوية الخارجية للمثلث هي الزاوية المجاورة لأي زاوية في هذا المثلث. أثبت أن الزاوية الخارجية للمثلث تساوي مجموع زاويتين غير مجاورتين للمثلث.
(رسم بياني 1)

حل:

دع Δ ABC ∠DAС يكون خارجيًا (الشكل 1). ثم ∠DAC = 180°-∠BAC (بخاصية الزوايا المجاورة)، حسب نظرية مجموع زوايا المثلث ∠B+∠C = 180°-∠BAC. من هذه التساويات نحصل على ∠DAС=∠В+∠С

حقيقة مثيرة للاهتمام:

مجموع زوايا المثلث " :

في هندسة لوباتشيفسكي، يكون مجموع زوايا المثلث دائمًا أقل من 180. وفي الهندسة الإقليدية يساوي دائمًا 180. في هندسة ريمان، مجموع زوايا المثلث دائمًا أكبر من 180.

من تاريخ الرياضيات:

يقدم إقليدس (القرن الثالث قبل الميلاد) في كتابه "العناصر" التعريف التالي: "الخطوط المتوازية هي خطوط تقع في نفس المستوى، وتمتد في كلا الاتجاهين إلى ما لا نهاية، ولا تلتقي ببعضها البعض على أي من الجانبين." .
بوسيدونيوس (القرن الأول قبل الميلاد) "خطان مستقيمان يقعان في نفس المستوى، متباعدان بشكل متساوٍ عن بعضهما البعض"
قدم العالم اليوناني القديم بابوس (القرن الثالث قبل الميلاد) رمز الخطوط المتوازية - العلامة =. وبعد ذلك، استخدم الاقتصادي الإنجليزي ريكاردو (1720-1823) هذا الرمز كعلامة يساوي.
فقط في القرن الثامن عشر بدأوا في استخدام الرمز للخطوط المتوازية - العلامة ||.
إن الاتصال الحي بين الأجيال لا ينقطع لحظة واحدة، فكل يوم نتعلم الخبرة التي راكمها أسلافنا. قام اليونانيون القدماء، بناءً على الملاحظات والخبرة العملية، باستخلاص النتائج والفرضيات المعبر عنها، ثم في اجتماعات العلماء - الندوات (حرفيًا "العيد") - حاولوا إثبات هذه الفرضيات وإثباتها. وحينها ظهرت المقولة: «الحق يولد في النزاع».

أسئلة:

1. ما هو المثلث؟
2. ماذا تقول نظرية مجموع زوايا المثلث؟
3. ما هي الزاوية الخارجية للمثلث؟

مجموع زوايا المثلث- موضوع مهم ولكنه بسيط إلى حد ما يتم تدريسه في هندسة الصف السابع. يتكون الموضوع من نظرية وبرهان قصير والعديد من النتائج المنطقية. ومعرفة هذا الموضوع تساعد في حل المسائل الهندسية في الدراسة اللاحقة للموضوع.

نظرية - ما هي زوايا المثلث التعسفي المضافة معًا؟

تنص النظرية على أنه إذا أخذت أي مثلث، بغض النظر عن نوعه، فإن مجموع زواياه سيكون دائمًا 180 درجة. ويتم إثبات ذلك على النحو التالي:

• على سبيل المثال، خذ المثلث ABC، ارسم خطًا مستقيمًا عبر النقطة B الموجودة في القمة وقم بتعيينه على أنه "a"، الخط المستقيم "a" يوازي تمامًا الجانب AC؛
• بين الخط المستقيم "أ" والجانبين AB وBC، يتم تحديد الزوايا ووضع علامة عليها بالرقمين 1 و2؛
• تعتبر الزاوية 1 مساوية للزاوية A، والزاوية 2 مساوية للزاوية C، حيث تعتبر هذه الزوايا متقاطعة؛
• وبالتالي، فإن المجموع بين الزوايا 1 و 2 و 3 (الذي تم تحديده بدلاً من الزاوية B) يتم التعرف عليه على أنه يساوي الزاوية المكشوفة مع الرأس B - وهو 180 درجة.

إذا كان مجموع الزوايا المشار إليها بالأرقام هو 180 درجة، فإن مجموع الزوايا A وB وC يتم التعرف عليه على أنه يساوي 180 درجة. هذه القاعدة صحيحة بالنسبة لأي مثلث.

ما يلي من النظرية الهندسية

من المعتاد تسليط الضوء على العديد من النتائج الطبيعية من النظرية المذكورة أعلاه.

• إذا كانت المسألة تتعلق بمثلث قائم الزاوية، فإن إحدى زواياه ستكون تساوي 90 درجة افتراضيًا، وسيكون مجموع الزوايا الحادة أيضًا 90 درجة.
• إذا كنا نتحدث عن مثلث متساوي الساقين قائم، فإن زواياه الحادة، والتي يصل مجموع قياساتها إلى 90 درجة، ستساوي بشكل فردي 45 درجة.
• يتكون المثلث متساوي الأضلاع من ثلاث زوايا متساوية، على التوالي، كل واحدة منها تساوي 60 درجة، ومجموعها سيكون 180 درجة.
• الزاوية الخارجية لأي مثلث ستكون مساوية للمجموع بين زاويتين داخليتين غير مجاورتين له.

يمكن استخلاص القاعدة التالية: أي مثلث له زاويتان حادتان على الأقل. في بعض الحالات، يتكون المثلث من ثلاث زوايا حادة، وإذا كان هناك اثنتين فقط، فإن الزاوية الثالثة ستكون منفرجة أو قائمة.

المثلث هو مضلع له ثلاثة جوانب (ثلاث زوايا). في أغلب الأحيان، تتم الإشارة إلى الجوانب بأحرف صغيرة تتوافق مع الأحرف الكبيرة التي تمثل القمم المقابلة. في هذه المقالة سوف نتعرف على أنواع هذه الأشكال الهندسية، وهي النظرية التي تحدد ما يساوي مجموع زوايا المثلث.

الأنواع حسب حجم الزاوية

تتميز الأنواع التالية من المضلعات ذات الرؤوس الثلاثة:

• حادة الزاوية، حيث تكون جميع الزوايا حادة؛
• مستطيل، له زاوية قائمة واحدة، تسمى مولداته الأرجل، والجانب الذي يقع مقابل الزاوية القائمة يسمى الوتر؛
• منفرج عندما واحد ;
• متساوي الساقين، وفيه يكون الضلعان متساويان، ويُسمَّيان جانبيين، والثالث هو قاعدة المثلث؛
• متساوي الأضلاع، مع وجود جميع الجوانب الثلاثة متساوية.

ملكيات

هناك خصائص أساسية مميزة لكل نوع من المثلثات:

• في مقابل الجانب الأكبر توجد دائمًا زاوية أكبر، والعكس صحيح؛
• على الجانبين المتساويين توجد زوايا متساوية، والعكس صحيح؛
• أي مثلث له زاويتان حادتان؛
• الزاوية الخارجية أكبر من أي زاوية داخلية غير مجاورة لها؛
• مجموع أي زاويتين يكون دائمًا أقل من 180 درجة؛
• الزاوية الخارجية تساوي مجموع الزاويتين الأخريين اللتين لا تتقاطعان معها.

نظرية مجموع زوايا المثلث

تنص النظرية على أنه إذا قمت بجمع كل زوايا الشكل الهندسي المعطى، والذي يقع على المستوى الإقليدي، فإن مجموعها سيكون 180 درجة. دعونا نحاول إثبات هذه النظرية.

دعونا نحصل على مثلث عشوائي ذو رؤوس KMN.

من خلال قمة الرأس M نرسم KN (يُسمى هذا الخط أيضًا الخط المستقيم الإقليدي). نحدد النقطة A عليها بحيث تقع النقطتان K و A على جوانب مختلفة من الخط المستقيم MH. نحصل على زاويتين متساويتين AMN وKNM، اللتين، مثل الزوايا الداخلية، تقعان بالعرض ويتم تشكيلهما بواسطة القاطع MN مع الخطين المستقيمين KH وMA، المتوازيين. ويترتب على ذلك أن مجموع زوايا المثلث الواقع عند القمم M و H يساوي حجم الزاوية KMA. تشكل الزوايا الثلاث مجموعًا يساوي مجموع الزوايا KMA وMKN. وبما أن هذه الزوايا داخلية أحادية الجانب بالنسبة إلى الخطين المستقيمين المتوازيين KN وMA مع قاطع KM، فإن مجموعهما يساوي 180 درجة. لقد تم إثبات النظرية.

عاقبة

النتيجة الطبيعية التالية تتبع النظرية المثبتة أعلاه: أي مثلث له زاويتان حادتان. لإثبات ذلك، لنفترض أن هذا الشكل الهندسي له زاوية حادة واحدة فقط. ويمكن أيضًا الافتراض أن أيًا من الزوايا ليست حادة. في هذه الحالة، يجب أن تكون هناك زاويتان على الأقل حجمهما يساوي أو يزيد عن 90 درجة. لكن مجموع قياسات الزوايا سيكون أكبر من 180 درجة. ولكن هذا لا يمكن أن يحدث، لأنه وفقا للنظرية فإن مجموع زوايا المثلث يساوي 180 درجة - لا أكثر ولا أقل. وهذا ما يجب إثباته.

خاصية الزوايا الخارجية

ما هو مجموع الزوايا الخارجية للمثلث؟ يمكن الحصول على إجابة هذا السؤال باستخدام إحدى الطريقتين. الأول: أنه لا بد من إيجاد مجموع الزوايا المأخوذة عند كل رأس زاوية واحدة، أي ثلاث زوايا. والثاني يعني أنك بحاجة إلى إيجاد مجموع زوايا الرأس الست. أولا، دعونا ننظر إلى الخيار الأول. إذن، المثلث يحتوي على ست زوايا خارجية - اثنتان عند كل رأس.

كل زوج له زوايا متساوية لأنها عمودية:

∟1 = ∟4, ∟2 = ∟5, ∟3 = ∟6.

ومن المعلوم أن الزاوية الخارجية للمثلث تساوي مجموع زاويتين داخليتين لا تتقاطعان معها. لذلك،

∟1 = ∟A + ∟C، ∟2 = ∟A + ∟B، ∟3 = ∟B + ∟C.

ومن هذا يتبين أن مجموع الزوايا الخارجية التي تؤخذ زاوية واحدة عند كل رأس سيكون مساوياً لما يلي:

∟1 + ∟2 + ∟3 = ∟A + ∟C + ∟A + ∟B + ∟B + ∟C = 2 x (∟A + ∟B + ∟C).

مع الأخذ في الاعتبار أن مجموع الزوايا يساوي 180 درجة، يمكننا القول أن ∟A + ∟B + ∟C = 180°. هذا يعني أن ∟1 + ∟2 + ∟3 = 2 × 180° = 360°. إذا تم استخدام الخيار الثاني، فسيكون مجموع الزوايا الست أكبر مرتين. أي أن مجموع الزوايا الخارجية للمثلث سيكون:

∟1 + ∟2 + ∟3 + ∟4 + ∟5 + ∟6 = 2 × (∟1 + ∟2 + ∟2) = 720°.

مثلث قائم

ما هو مجموع الزوايا الحادة للمثلث القائم؟ مرة أخرى، إجابة هذا السؤال تأتي من النظرية التي تنص على أن مجموع قياسات زوايا المثلث يساوي 180 درجة. وعبارتنا (الخاصية) تبدو هكذا: في المثلث القائم، مجموع الزوايا الحادة يصل إلى 90 درجة. دعونا نثبت صحتها.

دعونا نحصل على مثلث KMN، حيث ∟Н = 90°. من الضروري إثبات أن ∟К + ∟М = 90°.

لذلك، وفقًا لنظرية مجموع الزوايا ∟К + ∟М + ∟Н = 180°. شرطنا يقول أن ∟H = 90°. إذن اتضح أن ∟К + ∟М + 90° = 180°. أي ∟К + ∟М = 180° - 90° = 90°. وهذا هو بالضبط ما كنا بحاجة لإثباته.

بالإضافة إلى خصائص المثلث القائم الموضحة أعلاه، يمكنك إضافة ما يلي:

• الزوايا التي تقع مقابل الساقين حادة؛
• الوتر مثلثي أكبر من أي من الأرجل.
• مجموع الساقين أكبر من الوتر.
• إن ساق المثلث الذي يقع مقابل الزاوية التي قياسها 30 درجة، هي نصف حجم الوتر، أي تساوي نصفه.

وكخاصية أخرى لهذا الشكل الهندسي، يمكننا تسليط الضوء على نظرية فيثاغورس. وذكرت أنه في المثلث الذي قياس زاوية 90 درجة (مستطيل)، فإن مجموع مربعي الأرجل يساوي مربع الوتر.

مجموع زوايا المثلث متساوي الساقين

قلنا سابقًا أن المضلع المتساوي الساقين الذي له ثلاثة رؤوس ويحتوي على ضلعين متساويين يسمى. وهذه الخاصية لهذا الشكل الهندسي معروفة: الزوايا عند قاعدته متساوية. دعونا نثبت ذلك.

لنأخذ المثلث KMN، وهو متساوي الساقين، KN هي قاعدته.

نحن مطالبون بإثبات أن ∟К = ∟Н. لذا، لنفترض أن MA هو منصف مثلثنا KMN. المثلث MKA، مع الأخذ بعين الاعتبار علامة المساواة الأولى، يساوي المثلث MNA. أي أنه بشرط أن يكون KM = NM، MA هو الضلع المشترك، ∟1 = ∟2، نظرًا لأن MA منصف. باستخدام حقيقة أن هذين المثلثين متساويان، يمكننا القول أن ∟К = ∟Н. وهذا يعني أن النظرية قد تم إثباتها.

لكننا مهتمون بما هو مجموع زوايا المثلث (متساوي الساقين). وبما أنه في هذا الصدد ليس له خصائصه الخاصة، فسوف نبني على النظرية التي تمت مناقشتها سابقا. وهذا يعني أنه يمكننا القول أن ∟К + ∟М + ∟Н = 180°، أو 2 × ∟К + ∟М = 180° (بما أن ∟К = ∟Н). لن نثبت هذه الخاصية، حيث تم إثبات نظرية مجموع زوايا المثلث نفسه سابقًا.

بالإضافة إلى الخصائص التي تمت مناقشتها حول زوايا المثلث، تنطبق أيضًا العبارات المهمة التالية:

• الذي تم إنزاله على القاعدة، هو في نفس الوقت الوسيط، ومنصف الزاوية الواقعة بين الجانبين المتساويين، وكذلك قاعدتها؛
• المتوسطات (المنصفات، الارتفاعات) المرسومة على الجوانب الجانبية لهذا الشكل الهندسي متساوية.

مثلث متساوي الاضلاع

ويسمى أيضًا منتظمًا، وهو المثلث الذي تكون جميع أضلاعه متساوية. وبالتالي فإن الزوايا متساوية أيضًا. كل واحد 60 درجة. دعونا نثبت هذه الخاصية.

لنفترض أن لدينا مثلث KMN. نحن نعلم أن KM = NM = KN. هذا يعني أنه وفقًا لخاصية الزوايا الواقعة عند القاعدة في مثلث متساوي الساقين، ∟К = ∟М = ∟Н. نظرًا لأن مجموع زوايا المثلث، وفقًا للنظرية، هو ∟К + ∟М + ∟Н = 180°، ثم 3 x ∟К = 180° أو ∟К = 60°، ∟М = 60°، ∟ Н = 60°. وبذلك ثبت البيان.

كما يتبين من الدليل أعلاه بناءً على النظرية، فإن مجموع الزوايا، مثل مجموع زوايا أي مثلث آخر، هو 180 درجة. ليست هناك حاجة لإثبات هذه النظرية مرة أخرى.

هناك أيضًا خصائص مميزة للمثلث متساوي الأضلاع:

• يتطابق الوسيط والمنصف والارتفاع في هذا الشكل الهندسي، ويتم حساب طولهما على النحو التالي (a x √3): 2؛
• إذا وصفنا دائرة حول مضلع معين، فإن نصف قطرها سيكون مساويًا لـ (a x √3): 3؛
• إذا قمت بإدراج دائرة في مثلث متساوي الأضلاع، فسيكون نصف قطرها (a x √3): 6؛
• يتم حساب مساحة هذا الشكل الهندسي بالصيغة: (a2 x √3) : 4.

مثلث منفرج الزاوية

بحكم التعريف، إحدى زواياه تتراوح بين 90 و 180 درجة. لكن بما أن الزاويتين الأخريين لهذا الشكل الهندسي حادتان، فيمكننا أن نستنتج أن قياسهما لا يتجاوز 90 درجة. ولذلك فإن نظرية مجموع زوايا المثلث تعمل على حساب مجموع الزوايا في مثلث منفرج. اتضح أنه يمكننا القول بأمان، بناءً على النظرية المذكورة أعلاه، أن مجموع زوايا المثلث المنفرج يساوي 180 درجة. مرة أخرى، هذه النظرية لا تحتاج إلى إثبات مرة أخرى.

دليل

يترك اي بي سي" - مثلث تعسفي. دعونا نقود من خلال القمة ب خط موازي للخطمكيف الهواء (مثل هذا الخط المستقيم يسمى الخط المستقيم الإقليدي). دعونا نضع علامة على ذلكد بحيث النقاطأ ود تقع على جانبي متقابلين من خط مستقيم قبل الميلاد.الزوايا دي بي سيو ايه سي بييساوي الكذب الداخلي المتقاطع الذي يتكون من القاطع قبل الميلادمع خطوط متوازية مكيف الهواءو دينار بحريني. وبالتالي مجموع زوايا المثلث عند رؤوسه بو معيساوي الزاوية عبد.مجموع زوايا المثلث الثلاث يساوي مجموع زواياه عبدو باك. وبما أن هذه الزوايا داخلية من جانب واحد للتوازي مكيف الهواءو دينار بحرينيفي القاطع أ.بفيكون مجموعهما 180 درجة. لقد تم إثبات النظرية.

عواقب

ويترتب على هذه النظرية أن أي مثلث له زاويتان حادتان. في الواقع، باستخدام البرهان على التناقض، لنفترض أن المثلث له زاوية حادة واحدة فقط أو لا توجد زوايا حادة على الإطلاق. إذن هذا المثلث له زاويتان على الأقل، قياس كل منهما 90 درجة على الأقل. مجموع هذه الزوايا لا يقل عن 180 درجة. لكن هذا مستحيل، لأن مجموع زوايا المثلث هو 180 درجة. Q.E.D.

التعميم في النظرية البسيطة

أين هي الزاوية بين وجوه i ​​و j للبسيط.

ملحوظات

• على الكرة، مجموع زوايا المثلث يتجاوز دائمًا 180 درجة، ويسمى الفرق بالزيادة الكروية ويتناسب مع مساحة المثلث.
• في مستوى لوباتشيفسكي، يكون مجموع زوايا المثلث دائمًا أقل من 180 درجة. ويتناسب الفرق أيضًا مع مساحة المثلث.

أنظر أيضا

مؤسسة ويكيميديا. 2010.

• تايلور
• جسر نيجني ليبياجي

انظر ما هي "نظرية مجموع زوايا المثلث" في القواميس الأخرى:

نظرية مجموع زوايا المضلع- خاصية المضلعات في الهندسة الإقليدية: مجموع زوايا المثلث n هو 180°(n2). المحتويات 1 الدليل 2 ملاحظة ... ويكيبيديا

نظرية فيثاغورس- نظرية فيثاغورس هي إحدى النظريات الأساسية في الهندسة الإقليدية، والتي تحدد العلاقة بين أضلاع المثلث القائم الزاوية. المحتويات 1 ... ويكيبيديا

مساحة المثلث

نظرية فيثاغورس- نظرية فيثاغورس هي إحدى النظريات الأساسية في الهندسة الإقليدية، والتي تحدد العلاقة بين أضلاع المثلث القائم الزاوية. المحتويات 1 البيانات 2 الأدلة ... ويكيبيديا

نظرية جيب التمام- نظرية جيب التمام هي تعميم لنظرية فيثاغورس. مربع أحد أضلاع المثلث يساوي مجموع مربعي الضلعين الآخرين دون ضعف حاصل ضرب هذين الضلعين في جيب تمام الزاوية بينهما. للمثلث المستوي مع الجانبين أ، ب، جوالزاوية α... ... ويكيبيديا

مثلث- ولهذا المصطلح معاني أخرى، انظر المثلث (المعاني). المثلث (في الفضاء الإقليدي) هو شكل هندسي يتكون من ثلاثة أجزاء تربط ثلاث نقاط لا تقع على نفس الخط المستقيم. ثلاث نقاط،... ... ويكيبيديا

علامات المساواة في المثلثات- التدوين القياسي المثلث هو أبسط مضلع له 3 رؤوس (زوايا) و3 جوانب؛ جزء من المستوى يحده ثلاث نقاط لا تقع على نفس الخط وثلاثة أجزاء تربط هذه النقاط في أزواج. رؤوس المثلث ويكيبيديا

إقليدس- عالم رياضيات يوناني قديم. عمل في الإسكندرية في القرن الثالث. قبل الميلاد ه. العمل الرئيسي "المبادئ" (15 كتابا) يحتوي على أسس الرياضيات القديمة والهندسة الأولية ونظرية الأعداد والنظرية العامة للعلاقات وطريقة تحديد المساحات والأحجام،... ... القاموس الموسوعي

يوكليد- (توفي بين 275 و270 قبل الميلاد) عالم رياضيات يوناني قديم. لم تصلنا معلومات عن زمان ومكان ولادته ولكن من المعروف أن إقليدس عاش في الإسكندرية وكانت ذروة نشاطه في عهد بطليموس الأول في مصر... ... القاموس الموسوعي الكبير

الهندسة غير الإقليدية- هندسة تشبه الهندسة الإقليدية من حيث أنها تحدد حركة الأشكال، ولكنها تختلف عن الهندسة الإقليدية في أن إحدى مسلماتها الخمس (الثانية أو الخامسة) يتم استبدالها بنفيها. نفي إحدى المسلمات الإقليدية... موسوعة كولير

مثلث . المثلث الحاد والمنفرج والقائم.

الساقين والوتر. متساوي الساقين ومثلث متساوي الأضلاع.

مجموع زوايا المثلث.

الزاوية الخارجية للمثلث. علامات المساواة في المثلثات.

خطوط ونقاط ملحوظة في المثلث: الارتفاعات، والمتوسطات،

منصفات، متوسطه متعامدين,

مركز الثقل، مركز الدائرة المقيدة، مركز الدائرة المقيدة.

نظرية فيثاغورس. نسبة الارتفاع في مثلث تعسفي.

مثلث هو مضلع ذو ثلاثة جوانب (أو ثلاث زوايا). غالبًا ما تتم الإشارة إلى جوانب المثلث بأحرف صغيرة تتوافق مع الأحرف الكبيرة التي تمثل القمم المقابلة.

إذا كانت الزوايا الثلاث حادة (الشكل 20)، فهذا هو مثلث حاد الزوايا . إذا كانت إحدى الزوايا قائمة(ج، الشكل 21)، إنه مثلث قائم; الجانبينأ، بتسمى تشكيل الزاوية اليمنى الساقين; جانبجمقابل الزاوية اليمنى تسمى الوتر. إذا كان أحدزوايا منفرجة (ب، الشكل 22)، إنه مثلث منفرج الزاوية.


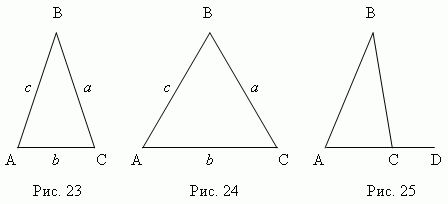
المثلث ABC (الشكل 23) - متساوي الساقين، لو اثنينأضلاعها متساوية (أ= ج); تسمى هذه الجوانب المتساوية جانبي، يتم استدعاء الطرف الثالث أساسمثلث. مثلث ABC (الشكل 24) – متساوي الاضلاع, لو الجميعأضلاعها متساوية (أ = ب = ج). على العموم ( أ ≠ ب ≠ ج) لدينا مختلف الأضلاعمثلث .

الخصائص الأساسية للمثلثات. في أي مثلث:

1. وفي مقابل الجانب الأكبر تقع الزاوية الأكبر، والعكس صحيح.

2. الزوايا المتساوية تقع مقابل جوانب متساوية، والعكس صحيح.

وعلى وجه الخصوص، جميع الزوايا في متساوي الاضلاعالمثلثان متساويان.

3. مجموع زوايا المثلث هو 180 º .

ويترتب على الخاصيتين الأخيرتين أن كل زاوية متساوية الأضلاع

المثلث هو 60 º.

4. استمرار أحد أضلاع المثلث (AC، الشكل 25)، نحن نحصل خارجي

زاوية بى سى دى . الزاوية الخارجية للمثلث تساوي مجموع الزوايا الداخلية،

لا مجاورة لها : بسد = أ + ب.

5. أي ضلع المثلث أقل من مجموع الضلعين الآخرين وأكبر

خلافاتهم (أ < ب + ج, أ > ب – ج;ب < أ + ج, ب > أ – ج;ج < أ + ب,ج > أ – ب).

علامات المساواة في المثلثات.

يتطابق المثلثان إذا كانا متساويين على الترتيب:

أ ) الضلعان والزاوية بينهما؛

ب ) الزاويتان والجانب المجاور لهما؛

ج) ثلاثة جوانب.

علامات المساواة في المثلثات القائمة.

اثنين مستطيلييكون المثلثان متساويين إذا تحقق أحد الشروط التالية:

1) أرجلهم متساوية؛

2) الساق والوتر في أحد المثلثات يساويان الساق والوتر في المثلث الآخر؛

3) الوتر والزاوية الحادة لمثلث واحد يساوي الوتر والزاوية الحادة للآخر؛

4) الساق والزاوية الحادة المجاورة لمثلث واحد تساوي الساق والزاوية الحادة المجاورة للمثلث الآخر؛

5) الساق والزاوية الحادة المقابلة لمثلث واحد متساويان مع الساق و الزاوية الحادة المقابلة للأخرى.

خطوط ونقاط رائعة في المثلث.

ارتفاع المثلث هوعمودي،خفضت من أي قمة إلى الجانب الآخر ( أو استمراره). ويسمى هذا الجانبقاعدة المثلث . الارتفاعات الثلاثة للمثلث تتقاطع دائمًافي نقطة واحدة، مُسَمًّى مركز تقويم العظاممثلث. مركز تقويم المثلث الحاد (النقطةيا ، الشكل 26) يقع داخل المثلث، ومركز تقويم المثلث المنفرج (النقطةيا ، الشكل 27) – الخارج؛ يتطابق مركز تقويم المثلث الأيمن مع قمة الزاوية القائمة.

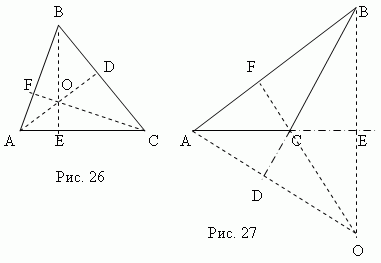
الوسيط - هذا القطعة المستقيمة ، يربط أي رأس للمثلث بمنتصف الضلع المقابل. ثلاثة متوسطات للمثلث (AD، BE، CF، الشكل 28) تتقاطع عند نقطة واحدة يا ، يقع دائمًا داخل المثلثويكون له مركز الجاذبية. تقسم هذه النقطة كل وسيط بنسبة 2:1، بدءًا من الرأس.

منصف - هذا قطعة منصفةالزاوية من الرأس إلى النقطة تقاطعات مع الجانب الآخر. ثلاثة منصفات المثلث (AD، BE، CF، الشكل 29) تتقاطع عند نقطة واحدة أوه، الكذب دائما داخل المثلثو كون مركز الدائرة المنقوشة(انظر قسم "مدرجوالمضلعات المقيدة").

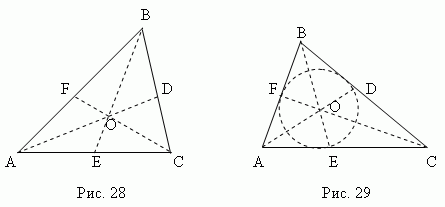
يقسم المنصف الجانب المقابل إلى أجزاء تتناسب مع الجوانب المجاورة ; على سبيل المثال، في الشكل 29 AE: CE = AB: قبل الميلاد.

متوسط ​​عمودي هو عمودي مرسوم من الوسطنقاط القطع (الجوانب). ثلاثة منصفات متعامدة للمثلث ABC(كو، مو، نو، الشكل 30 ) يتقاطعان عند نقطة واحدة O، وهي مركز دائرة مقيدة (النقاط K، M، N – منتصف أضلاع المثلثاي بي سي).

في المثلث حاد الزوايا، تقع هذه النقطة داخل المثلث؛ في منفرجة - في الخارج؛ في مستطيل - في منتصف الوتر. المركز المتعامد، مركز الثقل، المركز المحيطي والدائرة المنقوشة تتطابق فقط في مثلث متساوي الأضلاع.

نظرية فيثاغورس. في المثلث القائم مربع الطولالوتر يساوي مجموع مربعات أطوال الساقين.

إن إثبات نظرية فيثاغورس يأتي بوضوح من الشكل 31. فكر في مثلث قائم الزاوية ABC مع الساقين أ، بوالوتر ج.

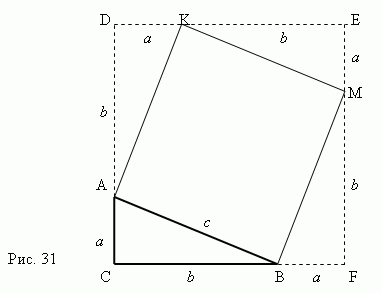
دعونا نبني مربعاأكمب باستخدام الوترأ.ب كجانب. ثممواصلة جوانب المثلث الأيمناي بي سي حتى تحصل على مربع CDEF ، الذي جانبه متساويأ + ب .والآن أصبح من الواضح أن مساحة الساحة CDEF يساوي ( أ + ب) 2 . ومن ناحية أخرى هذا المنطقة تساوي المجموعالمناطق أربعة مثلثات قائمةوالمربع AKMB، أي

ج 2 + 4 (أب / 2) = ج 2 + 2 أب,

من هنا،

ج 2 + 2 أب= (أ + ب) 2 ,

وأخيرا لدينا:

ج 2 =أ 2 + ب 2 .

نسبة الارتفاع في مثلث تعسفي.

في الحالة العامة (للمثلث التعسفي) لدينا:

ج 2 =أ 2 + ب 2 – 2أب· كوس ج،

أين سي - الزاوية بين الجانبينأو ب .