Mathematical analysis.

Workshop.

For university students in the specialty:

"State and municipal administration"

T.Z. Pavlova

Kolpashevo 2008

Chapter 1: Introduction to Analysis

1.1 Functions. General properties

1.2 Limit theory

1.3 Continuity of function

2.1 Definition of derivative

2.4 Function research

2.4.1 Full function study design

2.4.2 Function study examples

2.4.3. The largest and smallest value of a function on a segment

2.5 L'Hopital's rule

3.1 Indefinite integral

3.1.1 Definitions and properties

3.1.2 Table of integrals

3.1.3 Basic integration methods

3.2 Definite integral

3.2.2 Methods for calculating the definite integral

Chapter 4. Functions of several variables

4.1 Basic concepts

4.2 Limits and continuity of functions of several variables

4.3.3 Total differential and its application to approximate calculations

Chapter 5. Classical optimization methods

6.1 Utility function.

6.2 Lines of indifference

6.3 Budget set

Home test assignments

1.1 Functions. General properties

A numerical function is defined on the set D of real numbers if each value of the variable is associated with some well-defined real value of the variable y, where D is the domain of definition of the function.

Analytical representation of a function:

explicitly: ;

implicitly: ;

in parametric form:

different formulas in the area of definition:

Properties.

Even function: . For example, the function is even, because .

Odd function: . For example, the function is odd, because .

Periodic function: , where T is the period of the function, . For example, trigonometric functions.

Monotonic function. If for any of the domain of definition the function is increasing, then it is decreasing. For example, - increasing, and - decreasing.

Limited function. If there is a number M such that . For example, functions and , because .

Example 1. Find the domain of definition of the functions.

+ 2 – 3 +

1.2 Limit theory

Definition 1. The limit of a function at is a number b if for any ( is an arbitrarily small positive number) one can find a value of the argument starting from which the inequality holds.

Designation: .

Definition 2. The limit of a function at is a number b if for any ( is an arbitrarily small positive number) there is a positive number such that for all values of x satisfying the inequality the inequality is satisfied.

Designation: .

Definition 3. A function is said to be infinitesimal for or if or.

Properties.

1. The algebraic sum of a finite number of infinitesimal quantities is an infinitesimal quantity.

2. The product of an infinitesimal quantity and a bounded function (a constant, another infinitesimal quantity) is an infinitesimal quantity.

3. The quotient of dividing an infinitesimal quantity by a function whose limit is non-zero is an infinitesimal quantity.

Definition 4. A function is said to be infinitely large if .

Properties.

1. The product of an infinitely large quantity and a function whose limit is different from zero is an infinitely large quantity.

2. The sum of an infinitely large quantity and a limited function is an infinitely large quantity.

3. The quotient of dividing an infinitely large quantity by a function that has a limit is an infinitely large quantity.

Theorem.(The relationship between an infinitesimal quantity and an infinitely large quantity.) If a function is infinitesimal at (), then the function is an infinitely large quantity at (). And, conversely, if the function is infinitely large at (), then the function is an infinitesimal value at ().

Limit theorems.

1. A function cannot have more than one limit.

2. The limit of the algebraic sum of several functions is equal to the algebraic sum of the limits of these functions:

3. The limit of the product of several functions is equal to the product of the limits of these functions:

4. The limit of the degree is equal to the degree of the limit:

5. The limit of the quotient is equal to the quotient of the limits if the limit of the divisor exists:

6. The first wonderful limit.

Consequences:

7. Second remarkable limit:

Consequences:

Equivalent infinitesimal quantities at:

Calculation of limits.

When calculating limits, the basic theorems about limits, properties of continuous functions and rules arising from these theorems and properties are used.

Rule 1. To find the limit at a point of a function that is continuous at this point, you need to substitute its limit value into the function under the limit sign instead of the argument x.

Example 2. Find

Rule 2. If, when finding the limit of a fraction, the limit of the denominator is equal to zero, and the limit of the numerator is different from zero, then the limit of such a function is equal to .

Example 3. Find

Rule 3. If, when finding the limit of a fraction, the limit of the denominator is equal to , and the limit of the numerator is different from zero, then the limit of such a function is equal to zero.

Example 4. Find

Often, substituting the limit value of an argument results in undefined expressions of the form

Finding the limit of a function in these cases is called uncertainty discovery. To reveal the uncertainty, it is necessary to transform this expression before moving to the limit. Various techniques are used to reveal uncertainties.

Rule 4. The uncertainty of the type is revealed by transforming the sublimit function so that in the numerator and denominator one can isolate a factor whose limit is equal to zero, and, reducing the fraction by it, find the limit of the quotient. To do this, the numerator and denominator are either factored or multiplied by the expressions conjugate to the numerator and denominator.

Rule 5. If the sublimit expression contains trigonometric functions, then the first remarkable limit is used to resolve the uncertainty of the form.

Rule 6. To reveal the uncertainty of the form at , the numerator and denominator of the sublimit fraction must be divided by the highest power of the argument and then the limit of the quotient must be found.

Possible results:

1) the required limit is equal to the ratio of the coefficients of the highest powers of the argument of the numerator and denominator, if these powers are the same;

2) the limit is equal to infinity if the degree of the numerator argument is higher than the degree of the denominator argument;

3) the limit is equal to zero if the degree of the numerator argument is lower than the degree of the denominator argument.

because

The powers are equal, which means that the limit is equal to the ratio of the coefficients of the higher powers, i.e. .

The degree of the numerator and denominator is 1, which means the limit is

The degree of the numerator is 1, the denominator is , which means the limit is 0.

Rule 7. To reveal the uncertainty of the form, the numerator and denominator of the sublimit fraction must be multiplied by the conjugate expression.

Example 10.

Rule 8. To reveal the uncertainty of the species, the second remarkable limit and its consequences are used.

It can be proven that

Example 11.

Example 12.

Example 13.

Rule 9. When revealing uncertainties whose sublimit function contains b.m.v., it is necessary to replace the limits of these b.m.v. to the limits of b.m. equivalent to them.

Example 14.

Example 15.

Rule 10. L'Hopital's rule (see 2.6).

1.3 Continuity of function

A function is continuous at a point if the limit of the function, as the argument tends to a, exists and is equal to the value of the function at this point.

Equivalent conditions:

1. ;

Classification of break points:

1st kind rupture

Removable – one-sided limits exist and are equal;

Irreducible (jump) – one-sided limits are not equal;

discontinuity of the second kind: the limit of a function at a point does not exist.

Example 16. Establish the nature of the discontinuity of a function at a point or prove the continuity of a function at this point.

at the function is not defined, therefore, it is not continuous at this point. Because and correspondingly, , then is a point of removable discontinuity of the first kind.

Compared to assignment (a), the function is further defined at the point so that , which means that this function is continuous at this point.

When the function is not defined;

Because one of the one-sided limits is infinite, then this is a discontinuity point of the second kind.

Chapter 2. Differential calculus

2.1 Definition of derivative

Definition of derivative

The derivative or of a given function is the limit of the ratio of the increment of the function to the corresponding increment of the argument, when the increment of the argument tends to zero:

Or .

The mechanical meaning of a derivative is the rate of change of a function. The geometric meaning of the derivative is the tangent of the angle of inclination of the tangent to the graph of the function:

2.2 Basic rules of differentiation

Name	Function	Derivative
Multiplying by a constant factor
Algebraic sum of two functions
Product of two functions
Quotient of two functions
Complex function

Derivatives of basic elementary functions

No.	Function name	Function and its derivative
1	constant
2	power function special cases
3	exponential function special case
4	logarithmic function special case
5	trigonometric functions
6	reverse trigonometric

2.3 Higher order derivatives

Second order derivative of a function

Second order derivative of the function:

Example 18.

a) Find the second-order derivative of the function.

Solution. Let us first find the first order derivative .

From the first-order derivative, let us take the derivative again.

Example 19. Find the third-order derivative of the function.

2.4 Function research

2.4.1 Full function study plan:

Full function study plan:

1. Elementary research:

Find the domain of definition and range of values;

Find out general properties: evenness (oddness), periodicity;

Find the points of intersection with the coordinate axes;

Determine areas of constant sign.

2. Asymptotes:

Find vertical asymptotes if ;

Find oblique asymptotes: .

If any number, then – horizontal asymptotes.

3. Research using:

Find the critical points, those. points at which or does not exist;

Determine the intervals of increase, those. intervals on which the function decreases – ;

Determine extrema: points through which the sign changes from “+” to “–” are points of maximum, from “–” to “+” are points of minimum.

4. Research using:

Find points at which or does not exist;

Find areas of convexity, i.e. intervals on which and concavities – ;

Find inflection points, i.e. points when passing through which the sign changes.

1. Individual elements of the study are plotted on the graph gradually, as they are found.

2. If difficulties arise with constructing a graph of a function, then the values of the function are found at some additional points.

3. The purpose of the study is to describe the nature of the behavior of the function. Therefore, not an exact graph is built, but an approximation of it, on which the found elements are clearly marked (extrema, inflection points, asymptotes, etc.).

4. It is not necessary to strictly adhere to the given plan; It is important not to miss the characteristic elements of the function's behavior.

2.4.2 Examples of function research:

2) Odd function:

3) Asymptotes.

– vertical asymptotes, because

Oblique asymptote.

– inflection point.

2) Odd function:

3) Asymptotes: There are no vertical asymptotes.

Oblique:

– oblique asymptotes

4) – the function increases.

– inflection point.

Schematic graph of this function:

2) General function

3) Asymptotes

– there are no inclined asymptotes

– horizontal asymptote at

– inflection point

Schematic graph of this function:

2) Asymptotes.

– vertical asymptote, because

– there are no inclined asymptotes

, – horizontal asymptote

Schematic graph of this function:

2) Asymptotes

– vertical asymptote at , because

– there are no inclined asymptotes

, – horizontal asymptote

3) – the function decreases on each of the intervals.

Schematic graph of this function:

To find the largest and smallest values of a function on a segment, you can use the following diagram:

1. Find the derivative of the function.

2. Find the critical points of the function at which or does not exist.

3. Find the value of the function at critical points belonging to a given segment and at its ends and select the largest and smallest from them.

Example. Find the smallest and largest value of the function on a given segment.

25. in between

2) – critical points

26. in the interval.

The derivative does not exist for , but 1 does not belong to this interval. The function decreases on the interval, which means that there is no greatest value, but the smallest value is .

2.5 L'Hopital's rule

Theorem. The limit of the ratio of two infinitesimal or infinitely large functions is equal to the limit of the ratio of their derivatives (finite or infinite), if the latter exists in the indicated sense.

Those. when disclosing uncertainties of the type or you can use the formula:

27.

Chapter 3. Integral calculus

3.1 Indefinite integral

3.1.1 Definitions and properties

Definition 1. A function is called antiderivative for if .

Definition 2. An indefinite integral of a function f(x) is the set of all antiderivatives for this function.

Designation: , where c is an arbitrary constant.

Properties of the indefinite integral

1. Derivative of the indefinite integral:

2. Differential of the indefinite integral:

3. Indefinite integral of the differential:

4. Indefinite integral of the sum (difference) of two functions:

5. Extending the constant factor beyond the sign of the indefinite integral:

3.1.2 Table of integrals

.1.3 Basic integration methods

1. Using the properties of the indefinite integral.

Example 29.

2. Submitting the differential sign.

Example 30.

3. Variable replacement method:

a) replacement in the integral

Where - a function that is easier to integrate than the original one; - function inverse to function; - antiderivative of function.

Example 31.

b) replacement in the integral of the form:

Example 32.

Example 33.

4. Method of integration by parts:

Example 34.

Example 35.

Let us take separately the integral

Let's return to our integral:

3.2 Definite integral

3.2.1 The concept of a definite integral and its properties

Definition. Let a continuous function be given on a certain interval. Let's build a graph of it.

A figure bounded above by a curve, on the left and right by straight lines and below by a segment of the abscissa axis between points a and b is called a curvilinear trapezoid.

S – area – curvilinear trapezoid.

Divide the interval with dots and get:

Cumulative sum:

Definition. A definite integral is the limit of an integral sum.

Properties of the definite integral:

1. The constant factor can be taken out of the integral sign:

2. The integral of the algebraic sum of two functions is equal to the algebraic sum of the integrals of these functions:

3. If the integration segment is divided into parts, then the integral on the entire segment is equal to the sum of the integrals for each of the resulting parts, i.e. for any a, b, c:

4. If on the segment , then

5. The limits of integration can be swapped, and the sign of the integral changes:

7. The integral at the point is equal to 0:

9. (“about the mean”) Let y = f(x) be a function integrable on . Then , where , f(c) – average value of f(x) on:

10. Newton-Leibniz formula

where F(x) is the antiderivative of f(x).

3.2.2 Methods for calculating the definite integral.

1. Direct integration

Example 35.

2. Change of variables under the definite integral sign .

Example 36.

2. Integration by parts in a definite integral .

Example 37.

3.2.3 Applications of the definite integral

Characteristic	Function type	Formula
	in Cartesian coordinates
curvilinear sector area	in polar coordinates
area of a curved trapezoid	in parametric form
arc length	in Cartesian coordinates
arc length	in polar coordinates
arc length	in parametric form
body volume rotation	in Cartesian coordinates
volume of a body with a given transverse cross section

Example 38. Calculate the area of a figure bounded by lines: And .

Solution: Let's find the intersection points of the graphs of these functions. To do this, we equate the functions and solve the equation

So, the points of intersection and .

Find the area of the figure using the formula

In our case

Answer: Area is (square units).

4.1 Basic concepts

Definition. If each pair of mutually independent numbers from a certain set is assigned, according to some rule, one or more values of the variable z, then the variable z is called a function of two variables.

Definition. The domain of definition of a function z is the set of pairs for which the function z exists.

The domain of definition of a function of two variables is a certain set of points on the Oxy coordinate plane. The z coordinate is called an applicate, and then the function itself is depicted as a surface in the space E 3 . For example:

Example 39. Find the domain of the function.

The expression on the right side makes sense only when . This means that the domain of definition of this function is the set of all points lying inside and on the boundary of a circle of radius R with a center at the origin.

The domain of definition of this function is all points of the plane, except points of straight lines, i.e. coordinate axes.

Definition. Function level lines are a family of curves on the coordinate plane, described by equations of the form.

Example 40. Find function level lines .

Solution. The level lines of a given function are a family of curves on the plane, described by the equation

The last equation describes a family of circles with a center at point O 1 (1, 1) of radius . The surface of revolution (paraboloid) described by this function becomes “steeper” as it moves away from the axis, which is given by the equations x = 1, y = 1. (Fig. 4)

4.2 Limits and continuity of functions of several variables.

1. Limits.

Definition. A number A is called the limit of a function as a point tends to a point if for every arbitrarily small number there is a number such that for any point the condition is true, and the condition is also true . Write down: .

Example 41. Find limits:

those. the limit depends on , which means it does not exist.

2. Continuity.

Definition. Let the point belong to the domain of definition of the function. Then a function is called continuous at a point if

(1)

and the point tends to the point in an arbitrary manner.

If at any point condition (1) is not satisfied, then this point is called the break point of the function. This may be in the following cases:

1) The function is not defined at point .

2) There is no limit.

3) This limit exists, but it is not equal to .

Example 42. Determine whether a given function is continuous at the point if .

Got that This means that this function is continuous at the point.

the limit depends on k, i.e. it does not exist at this point, which means the function has a discontinuity at this point.

4.3 Derivatives and differentials of functions of several variables

4.3.1 First order partial derivatives

The partial derivative of a function with respect to the argument x is the ordinary derivative of a function of one variable x for a fixed value of the variable y and is denoted:

The partial derivative of a function with respect to the argument y is the ordinary derivative of a function of one variable y for a fixed value of the variable x and is denoted:

Example 43. Find partial derivatives of functions.

4.3.2 Second order partial derivatives

Second order partial derivatives are partial derivatives of first order partial derivatives. For a function of two variables of the form, four types of second-order partial derivatives are possible:

Second-order partial derivatives, in which differentiation is carried out with respect to different variables, are called mixed derivatives. The second order mixed derivatives of a twice differentiable function are equal.

Example 44. Find second-order partial derivatives.

4.3.3 Total differential and its application to approximate calculations.

Definition. The first order differential of a function of two variables is found by the formula

Example 45. Find the complete differential for the function.

Solution. Let's find the partial derivatives:

For small increments of arguments x and y, the function receives an increment approximately equal to dz, i.e. .

Formula for finding the approximate value of a function at a point if its exact value at a point is known:

Example 46. Find .

Solution. Let ,

Then we use the formula

Answer. .

Example 47. Calculate approximately .

Solution. Let's consider the function. We have

Example 48. Calculate approximately .

Solution. Consider the function . We get:

Answer. .

4.3.4 Differentiation of an implicit function

Definition. A function is called implicit if it is given by an equation that is not solvable with respect to z.

The partial derivatives of such a function are found by the formulas:

Example 49: Find the partial derivatives of the function z given by the equation .

Solution.

Definition. A function is called implicit if it is given by an equation that is not solvable with respect to y.

The derivative of such a function is found by the formula:

Example 50. Find derivatives of these functions.

5.1 Local extremum of a function of several variables

Definition 1. A function has a maximum at point if

Definition 2. A function has a minimum at point if for all points sufficiently close to the point and different from it.

A necessary condition for an extremum. If a function reaches an extremum at a point, then the partial derivatives of the function vanish or do not exist at that point.

The points at which partial derivatives vanish or do not exist are called critical.

A sufficient sign of an extremum. Let the function be defined in some neighborhood of the critical point and have continuous second-order partial derivatives at this point

1) has a local maximum at the point if and ;

2) has a local minimum at the point if and ;

3) does not have a local extremum at the point if ;

Scheme of research on the extremum of a function of two variables.

1. Find the partial derivatives of the functions: and.

2. Solve the system of equations and find the critical points of the function.

3. Find second-order partial derivatives, calculate their values at critical points and, using a sufficient condition, draw a conclusion about the presence of extrema.

4. Find the extrema of the function.

Example 51. Find extrema of a function .

1) Let's find the partial derivatives.

2) Let's solve the system of equations

4) Let us find the second order partial derivatives and their values at critical points: . At the point we get:

This means that there is no extremum at the point. At the point we get:

This means that there is a minimum at the point.

5.2 Global extremum (the largest and smallest value of the function)

The largest and smallest values of a function of several variables, continuous on some closed set, are achieved either at extremum points or at the boundary of the set.

Scheme for finding the largest and smallest values.

1) Find critical points lying inside the region, calculate the value of the function at these points.

2) Investigate the function at the boundary of the region; if the border consists of several different lines, then the study must be carried out for each section separately.

3) Compare the obtained function values and select the largest and smallest.

Example 52. Find the largest and smallest values of a function in a rectangle.

Solution. 1) Let’s find the critical points of the function, for this we’ll find the partial derivatives: , and solve the system of equations:

We have obtained a critical point A. The resulting point lies inside the given region,

The boundary of the region is made up of four segments: i. Let's find the largest and smallest value of the function on each segment.

4) Let us compare the results obtained and find that at the points .

Chapter 6. Model of consumer choice

We will assume that there are n different goods. Then we will denote a certain set of goods by an n-dimensional vector , where is the quantity of the i-th product. The set of all sets of goods X is called a space.

The choice of an individual consumer is characterized by a relationship of preference: it is believed that the consumer can say about any two sets which is more desirable, or he does not see the difference between them. The preference relation is transitive: if a set is preferable to a set, and a set is preferable to a set, then the set is preferable to a set. We will assume that consumer behavior is completely described by the axiom of the individual consumer: each individual consumer makes decisions about consumption, purchases, etc., based on his system of preferences.

6.1 Utility function

A function is defined on the set of consumer sets X , the value of which on the consumer set is equal to the individual’s consumer assessment for this set. The function is called the consumer utility function or consumer preference function. Those. Each consumer has his own utility function. But the entire set of consumers can be divided into certain classes of consumers (by age, property status, etc.) and each class can be assigned a certain, perhaps averaged, utility function.

Thus, the function is a consumer assessment or the level of satisfaction of an individual’s needs when purchasing a given set. If a set is preferable to a set for a given individual, then .

Properties of the utility function.

The first partial derivatives of the utility function are called marginal utilities of products. From this property it follows that an increase in the consumption of one product while the consumption of other products remains unchanged leads to an increase in consumer evaluation. Vector is the gradient of the function, it shows the direction of greatest growth of the function. For a function, its gradient is a vector of marginal utilities of products.

Those. The marginal utility of any good decreases as consumption increases.

Those. The marginal utility of each product increases as the quantity of the other product increases.

Some types of utility functions.

1) Neoclassical: .

2) Quadratic: , where the matrix is negative definite and For .

3) Logarithmic function: .

6.2 Lines of indifference

In applied problems and models of consumer choice, a special case of a set of two goods is often used, i.e. when the utility function depends on two variables. The line of indifference is a line connecting consumer sets that have the same level of satisfaction of the individual's needs. In essence, indifference lines are function level lines. Equations of indifference lines: .

Basic properties of indifference lines.

1. Lines of indifference corresponding to different levels of need satisfaction do not touch or intersect.

2. Lines of indifference decrease.

3. Indifference lines are convex downwards.

Property 2 implies an important approximate equality.

This ratio shows how much an individual should increase (decrease) the consumption of the second product when decreasing (increasing) the consumption of the first product by one unit without changing the level of satisfaction of his needs. The ratio is called the rate of replacement of the first product by the second, and the value is called the marginal rate of replacement of the first product by the second.

Example 53. If the marginal utility of the first good is 6, and the second is 2, then if the consumption of the first good is reduced by one unit, the consumption of the second good must be increased by 3 units at the same level of satisfaction of needs.

6.3 Budget set

Let – vector of prices for a set of n products; I is the individual’s income, which he is willing to spend on purchasing a set of products. The set of sets of goods costing no more than I at given prices is called the budget set B. Moreover, the set of sets costing I is called the boundary G of the budget set B. Thus. the set B is bounded by the boundary G and natural restrictions.

The budget set is described by a system of inequalities:

For the case of a set of two goods, the budget set B (Fig. 1) is a triangle in the coordinate system, limited by the coordinate axes and the straight line.

6.4 Theory of consumer demand

In consumption theory, it is believed that the consumer always strives to maximize his utility and the only limitation for him is the limited income I that he can spend on purchasing a set of goods. In general, the problem of consumer choice (the problem of rational consumer behavior in the market) is formulated as follows: find the consumer set , which maximizes its utility function under a given budget constraint. Mathematical model of this problem:

In the case of a set of two products:

Geometrically, the solution to this problem is the point of tangency between the boundary of the budget set G and the indifference line.

The solution to this problem comes down to solving the system of equations:

(1)

The solution to this system is the solution to the consumer choice problem.

The solution to the consumer choice problem is called the demand point. This point of demand depends on prices and income I. I.e. the demand point is a function of demand. In turn, the demand function is a set of n functions, each of which depends on an argument:

These functions are called demand functions for the corresponding goods.

Example 54. For a set of two goods on the market, known prices for them and income I, find the demand functions if the utility function has the form .

Solution. Let's differentiate the utility function:

Let us substitute the resulting expressions into (1) and obtain a system of equations:

In this case, the expense for each product will be half of the consumer’s income, and the quantity of the product purchased is equal to the amount spent on it divided by the price of the product.

Example 55. Let the utility function for the first good, second,

price of the first product, price of the second. Income . How much of a good should a consumer purchase to maximize utility?

Solution. Let's find the derivatives of the utility functions, substitute them into system (1) and solve it:

This set of goods is optimal for the consumer from the point of view of maximizing utility.

The test must be completed in accordance with the option selected by the last digit of the grade book number in a separate notebook. Each problem must contain a condition, a detailed solution and a conclusion.

1. Introduction to mathematical analysis

Task 1. Find the domain of definition of the function.

Task 2. Find the limits of the functions.

Task 3. Find the discontinuity points of the function and determine their type.

1. 2. 3.

Chapter 2. Differential calculus of a function of one variable

Task 4. Find derivatives of these functions.

1. a); b) c) y = ;

d) y = x 6 + + + 5; e) y = x tan x + ln sin x + e 3x ;

e) y = 2 x - arcsin x.

2. a) ; b) y = ; c) y = ; d) y = x 2 –+ 3; e) y = e cos; e) y = .

3. a) y = lnx; b) y =; c) y = ln;

4. a) y = ; b) y = (e 5 x – 1) 6 ; c) y = ; d) y = ; e) y = x 8 ++ + 5; e) y = 3 x - arcsin x.

5. a) y = 2x 3 - + e x ; b) y = ; c) y = ;

d) y = ; e) y = 2 cos; e) y = .

6. a) y = lnx; b) y =; c) y = ln;

d) y = ; e) y = x 7 + + 1; e) y = 2.

7. a) ; b) y = ; c)y = ; d)y = x 2 + xsinx + ; e) y = e cos; e) y = .

8. a) y = ; b) y = (3 x – 4) 6 ; c) y = sintg;

d) y = 3x 4 – – 9+ 9; e) y = ;

e)y = x 2 + arcsin x - x.

9. a); b) ; c) y = ; d) y = 5 sin 3 x ; e) y = x 3 – – 6+ 3; e) y = 4x 4 + ln.

10. a) b) y = ; c) y = (3 x – 4) 6 ; d) y = ; e)y = x 2 - x; e) y = e sin 3 x + 2.

Task 5. Explore the function and build its graph.

1. a) b) c) .

2. a) b) V) .

3. a) b) V) .

4. b) V)

5. a) b) V) .

6. a) b) V) .

7. a) b) c) .

8. a) b) c) .

9. a) b) c) .

10. a) b) V) .

Task 6. Find the largest and smallest value of the function on a given segment.

1. .

3. .

6. .

8. .

9. .

10. .

Chapter 3. Integral calculus

Problem 7. Find indefinite integrals.

1. a) b);

2. a) ;b) c) d) .

4. G)

5. a) ; b); V) ; G).

6. a) ; b); V); G)

7. a) ; b) ; V) ; G)

8. a) ; b); V) ; G) .

9. a) ; b) c); G).

10. a) b) V) ; G) .

Problem 8. Calculate definite integrals.

7. .

10.

Problem 9. Find improper integrals or prove that they diverge.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

Problem 10. Find the area of the region bounded by the curves

1. .2. .

5. 6.

7. , .8..

10. , .

Chapter 4. Differential calculus of functions of several variables.

Task 11. Find the domain of definition of the function (show in the drawing).

Problem 12. Investigate the continuity of the function at

Problem 13. Find the derivative of an implicitly given function.

Problem 14. Calculate approximately

1. a) ;b) ; V)

2. a) ; b) ; V) .

3. a) ; b) ; V) .

4. a) ; b) ; V) .

5. a); b) ; V) .

6. a); b) ; V) .

7. a); b) ; V) .

8. a) ;b) ; V)

9. a) ; b) ; V) .

10. a) ;b) ; V)

Problem 15. Investigate the function for extrema.

7. .

8. .

9. .

10. .

Problem 16. Find the largest and smallest value of the function in a given closed region.

1. in a rectangle

3. in a rectangle

4. in the area limited by a parabola

And the x-axis.

5. squared

6. in a triangle limited by the coordinate axes and the straight line

7. in a triangle limited by the coordinate axes and the straight line

8. in a triangle bounded by the coordinate axes and the straight line

9. in the area limited by a parabola

And the x-axis.

10. in the area limited by a parabola

And the x-axis.

Main

1. M.S. Krass, B.P. Chuprynov. Fundamentals of mathematics and its application in economic education: Textbook. – 4th ed., Spanish. – M.: Delo, 2003.

2. M.S. Krass, B.P. Chuprynov. Mathematics for economic specialties: Textbook. – 4th ed., Spanish. – M.: Delo, 2003.

3. M.S. Krass, B.P. Chuprynov. Mathematics for economic bachelor's degree. Textbook. – 4th ed., Spanish. – M.: Delo, 2005.

4. Higher mathematics for economists. Textbook for universities / N.Sh. Kremer, B.A. Putko, I.M. Trishin, M.N. Friedman; Ed. prof. N.Sh. Kremer, - 2nd ed., revised. and additional – M: UNITY, 2003.

5. Kremer N.Sh., Putko B.A., Trishin I.M., Fridman M.N.. Higher mathematics for economic specialties. Textbook and Workshop (parts I and II) / Ed. prof. N.Sh. Kremer, - 2nd ed., revised. and additional – M: Higher Education, 2007. – 893 p. – (Fundamentals of Sciences)

6. Danko P.E., Popov A.G., Kozhevnikova T.Ya. Higher mathematics in exercises and problems. M. Higher School. 1999.

Additional

1. I.I. Bavrin, V.L. Sailors. Higher mathematics. "Humanitarian Publishing Center Vlados", 2002.

2. I.A. Zaitsev. Higher mathematics. "Higher School", 1998.

3. A.S. Solodovnikov, V.A. Babaytsev, A.V. Brailov, I.G. Shandra. Mathematics in economics / in two parts/. M. Finance and Statistics. 1999.

Solving physical problems or examples in mathematics is completely impossible without knowledge of the derivative and methods for calculating it. The derivative is one of the most important concepts in mathematical analysis. We decided to devote today’s article to this fundamental topic. What is a derivative, what is its physical and geometric meaning, how to calculate the derivative of a function? All these questions can be combined into one: how to understand the derivative?

Geometric and physical meaning of derivative

Let there be a function f(x) , specified in a certain interval (a, b) . Points x and x0 belong to this interval. When x changes, the function itself changes. Changing the argument - the difference in its values x-x0 . This difference is written as delta x and is called argument increment. A change or increment of a function is the difference between the values of a function at two points. Definition of derivative:

The derivative of a function at a point is the limit of the ratio of the increment of the function at a given point to the increment of the argument when the latter tends to zero.

Otherwise it can be written like this:

What's the point of finding such a limit? And here's what it is:

the derivative of a function at a point is equal to the tangent of the angle between the OX axis and the tangent to the graph of the function at a given point.

Physical meaning of the derivative: the derivative of the path with respect to time is equal to the speed of rectilinear motion.

Indeed, since school days everyone knows that speed is a particular path x=f(t) and time t . Average speed over a certain period of time:

To find out the speed of movement at a moment in time t0 you need to calculate the limit:

Rule one: set a constant

The constant can be taken out of the derivative sign. Moreover, this must be done. When solving examples in mathematics, take it as a rule - If you can simplify an expression, be sure to simplify it .

Example. Let's calculate the derivative:

Rule two: derivative of the sum of functions

The derivative of the sum of two functions is equal to the sum of the derivatives of these functions. The same is true for the derivative of the difference of functions.

We will not give a proof of this theorem, but rather consider a practical example.

Find the derivative of the function:

Rule three: derivative of the product of functions

The derivative of the product of two differentiable functions is calculated by the formula:

Example: find the derivative of a function:

Solution:

It is important to talk about calculating derivatives of complex functions here. The derivative of a complex function is equal to the product of the derivative of this function with respect to the intermediate argument and the derivative of the intermediate argument with respect to the independent variable.

In the above example we come across the expression:

In this case, the intermediate argument is 8x to the fifth power. In order to calculate the derivative of such an expression, we first calculate the derivative of the external function with respect to the intermediate argument, and then multiply by the derivative of the intermediate argument itself with respect to the independent variable.

Rule four: derivative of the quotient of two functions

Formula for determining the derivative of the quotient of two functions:

We tried to talk about derivatives for dummies from scratch. This topic is not as simple as it seems, so be warned: there are often pitfalls in the examples, so be careful when calculating derivatives.

With any questions on this and other topics, you can contact the student service. In a short time, we will help you solve the most difficult test and understand the tasks, even if you have never done derivative calculations before.

for students medical, pediatric, dental

and medical and preventive faculties

to laboratory work

"Basic concepts of mathematical analysis"

1. Scientific and methodological substantiation of the topic:

The concepts of derivative and differential are among the basic concepts of mathematical analysis. Calculation of derivatives is necessary when solving many problems in physics and mathematics (finding speed, acceleration, pressure, etc.). The importance of the concept of derivative, in particular, is determined by the fact that the derivative of a function characterizes the rate of change of this function when its argument changes.

The use of a differential allows for approximate calculations, as well as error assessment.

Methods for finding derivatives and differentials of functions and their application constitute the main task of differential calculus. The need for the concept of derivative arises in connection with the formulation of the problem of calculating the speed of movement and finding the angle of the tangent to the curve. The inverse problem is also possible: using the speed to determine the distance traveled, and using the tangent of the tangent angle to find the corresponding function. This inverse problem leads to the concept of an indefinite integral.

The concept of a definite integral is used in a number of practical problems, in particular in problems of calculating the areas of plane figures, calculating the work done by a variable force, and finding the average value of a function.

When mathematically describing various physical, chemical, biological processes and phenomena, equations are often used that contain not only the quantities being studied, but also their derivatives of various orders of these quantities. For example, according to the simplest version of the law of bacterial reproduction, the rate of reproduction is proportional to the number of bacteria at a given time. If this quantity is denoted by N(t), then, in accordance with the physical meaning of the derivative, the rate of bacterial reproduction is a derivative of N(t), and based on the mentioned law, we can write the relation N"(t)=k∙N, where k>0 - coefficient of proportionality. The resulting equation is not algebraic, since it contains not only the unknown function N(t), but also its first-order derivative.

2. Brief theory:

1. Problems leading to the concept of derivative

1. The problem of finding the velocity v of a material point. Let some material point perform rectilinear motion. At a moment in time t 1 the point is in position M 1. At a moment in time t 2 pregnant M 2 . Let us denote the interval M 1 , M 2 through ΔS; t 2 – t 1 =Δt. The value is called the average speed of movement. To find the instantaneous speed of a point at a position M 1 necessary Δt rush towards zero. Mathematically this means that

, (1)

Thus, to find the instantaneous velocity of a material point, it is necessary to calculate the limit of the ratio of the increment of the function ΔS to the increment of the argument Δt, provided that Δt→0.

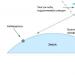
2. The problem of finding the angle of inclination of the tangent to the graph of a function.

Fig.1

Consider the graph of some function y=f(x). What is the angle of inclination?
tangent drawn at a point M 1 ? At the point M 1 Let's draw a tangent to the graph of the function. Select an arbitrary point on the graph M 2 and draw a secant. It is tilted to the axis OH at an angle α 1 . Let's consider ΔM 1 M 2 A:

, (2)

If the point M 1 fix and point M 2 bring closer to M 1 , then the secant M 1 M 2 will go tangent to the graph of the function at the point M 1 and we can write:

, (3)

Thus, it is necessary to calculate the limit of the ratio of the function increment to the argument increment if the argument increment tends to zero.

Limit of the ratio of the increment Δy of the function y=f(x) to the increment of the argument Δx at a given point x 0 as Δx tends to zero, is called the derivative of the function at a given point.

Derivative notation: y", f "(x), . A-priory

, (4)

where Δx=х 2 -х 1 is the increment of the argument (the difference between two subsequent fairly close values of the argument), Δy=y 2 -y 1 is the increment of the function (the difference between the values of the function corresponding to these values of the argument).

Finding the derivative of a given function is called its differentiation. Differentiation of the main elementary functions is carried out using ready-made formulas (see table), as well as using rules:

Derivative of an algebraic sum functions is equal to the sum of the derivatives of these functions:

(u+ υ )"= u" + υ "

2. The derivative of the product of two functions is equal to the sum of the products of the second function and the derivative of the first and the first function and the derivative of the second:

(u∙υ )"=u"υ +uυ "

3. Derivative of the quotient two functions is equal to a fraction, the numerator of which is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the denominator:

Physical meaning of the derivative. From a comparison of (4) and (1) it follows that the instantaneous speed of rectilinear motion of a material point is equal to the derivative of the dependence of its coordinate on time.

The general meaning of the derivative of a function is that it characterizes rate (speed) of change of a function for a given change in argument. The speed of physical, chemical and other processes, for example the rate of cooling of the body, the rate of a chemical reaction, the rate of reproduction of bacteria, etc., is also expressed using a derivative.

Geometric meaning of derivative. The value of the tangent of the angle of inclination of a tangent drawn to the graph of a function is called in mathematics tangent angular coefficient.

The angular coefficient of the tangent drawn to the graph of the differentiable function at a certain point is numerically equal to the derivative of the function at this point.

This statement is called geometric meaning of derivative.

On which we examined the simplest derivatives, and also became acquainted with the rules of differentiation and some technical techniques for finding derivatives. Thus, if you are not very good with derivatives of functions or some points in this article are not entirely clear, then first read the above lesson. Please get in a serious mood - the material is not simple, but I will still try to present it simply and clearly.

In practice, you have to deal with the derivative of a complex function very often, I would even say, almost always, when you are given tasks to find derivatives.

We look at the table at the rule (No. 5) for differentiating a complex function:

Let's figure it out. First of all, let's pay attention to the entry. Here we have two functions - and , and the function, figuratively speaking, is nested within the function . A function of this type (when one function is nested within another) is called a complex function.

I will call the function external function, and the function – internal (or nested) function.

! These definitions are not theoretical and should not appear in the final design of assignments. I use informal expressions “external function”, “internal” function only to make it easier for you to understand the material.

To clarify the situation, consider:

Example 1

Find the derivative of a function

Under the sine we have not just the letter “X”, but an entire expression, so finding the derivative right away from the table will not work. We also notice that it is impossible to apply the first four rules here, there seems to be a difference, but the fact is that the sine cannot be “torn into pieces”:

In this example, it is already intuitively clear from my explanations that a function is a complex function, and the polynomial is an internal function (embedding), and an external function.

First step what you need to do when finding the derivative of a complex function is to understand which function is internal and which is external.

In the case of simple examples, it seems clear that a polynomial is embedded under the sine. But what if everything is not obvious? How to accurately determine which function is external and which is internal? To do this, I suggest using the following technique, which can be done mentally or in a draft.

Let's imagine that we need to calculate the value of the expression at on a calculator (instead of one there can be any number).

What will we calculate first? First of all you will need to perform the following action: , therefore the polynomial will be an internal function:

Secondly will need to be found, so sine – will be an external function:

After we SOLD OUT with internal and external functions, it’s time to apply the rule of differentiation of complex functions .

Let's start deciding. From the lesson How to find the derivative? we remember that the design of a solution to any derivative always begins like this - we enclose the expression in brackets and put a stroke at the top right:

At first we find the derivative of the external function (sine), look at the table of derivatives of elementary functions and notice that . All table formulas are also applicable if “x” is replaced with a complex expression, in this case:

Please note that the inner function hasn't changed, we don't touch it.

Well, it's quite obvious that

The result of applying the formula in its final form it looks like this:

The constant factor is usually placed at the beginning of the expression:

If there is any misunderstanding, write the solution down on paper and read the explanations again.

Example 2

Find the derivative of a function

Example 3

Find the derivative of a function

As always, we write down:

Let's figure out where we have an external function and where we have an internal one. To do this, we try (mentally or in a draft) to calculate the value of the expression at . What should you do first? First of all, you need to calculate what the base is equal to: therefore, the polynomial is the internal function:

And only then is the exponentiation performed, therefore, the power function is an external function:

According to the formula , first you need to find the derivative of the external function, in this case, the degree. We look for the required formula in the table: . We repeat again: any tabular formula is valid not only for “X”, but also for a complex expression. Thus, the result of applying the rule for differentiating a complex function next:

I emphasize again that when we take the derivative of the external function, our internal function does not change:

Now all that remains is to find a very simple derivative of the internal function and tweak the result a little:

Example 4

Find the derivative of a function

This is an example for you to solve on your own (answer at the end of the lesson).

To consolidate your understanding of the derivative of a complex function, I will give an example without comments, try to figure it out on your own, reason where the external and where the internal function is, why the tasks are solved this way?

Example 5

a) Find the derivative of the function

b) Find the derivative of the function

Example 6

Find the derivative of a function

Here we have a root, and in order to differentiate the root, it must be represented as a power. Thus, first we bring the function into the form appropriate for differentiation:

Analyzing the function, we come to the conclusion that the sum of the three terms is an internal function, and raising to a power is an external function. We apply the rule of differentiation of complex functions :

We again represent the degree as a radical (root), and for the derivative of the internal function we apply a simple rule for differentiating the sum:

Ready. You can also reduce the expression to a common denominator in brackets and write everything down as one fraction. It’s beautiful, of course, but when you get cumbersome long derivatives, it’s better not to do this (it’s easy to get confused, make an unnecessary mistake, and it will be inconvenient for the teacher to check).

Example 7

Find the derivative of a function

This is an example for you to solve on your own (answer at the end of the lesson).

It is interesting to note that sometimes instead of the rule for differentiating a complex function, you can use the rule for differentiating a quotient , but such a solution will look like an unusual perversion. Here is a typical example:

Example 8

Find the derivative of a function

Here you can use the rule of differentiation of the quotient , but it is much more profitable to find the derivative through the rule of differentiation of a complex function:

We prepare the function for differentiation - we move the minus out of the derivative sign, and raise the cosine into the numerator:

Cosine is an internal function, exponentiation is an external function.
Let's use our rule :

We find the derivative of the internal function and reset the cosine back down:

Ready. In the example considered, it is important not to get confused in the signs. By the way, try to solve it using the rule , the answers must match.

Example 9

Find the derivative of a function

This is an example for you to solve on your own (answer at the end of the lesson).

So far we have looked at cases where we had only one nesting in a complex function. In practical tasks, you can often find derivatives, where, like nesting dolls, one inside the other, 3 or even 4-5 functions are nested at once.

Example 10

Find the derivative of a function

Let's understand the attachments of this function. Let's try to calculate the expression using the experimental value. How would we count on a calculator?

First you need to find , which means the arcsine is the deepest embedding:

This arcsine of one should then be squared:

And finally, we raise seven to a power:

That is, in this example we have three different functions and two embeddings, while the innermost function is the arcsine, and the outermost function is the exponential function.

Let's start deciding

According to the rule First you need to take the derivative of the outer function. We look at the table of derivatives and find the derivative of the exponential function: The only difference is that instead of “x” we have a complex expression, which does not negate the validity of this formula. So, the result of applying the rule for differentiating a complex function next.